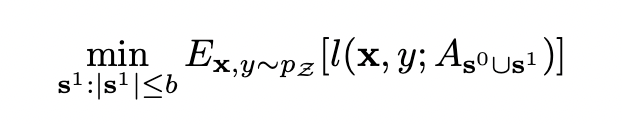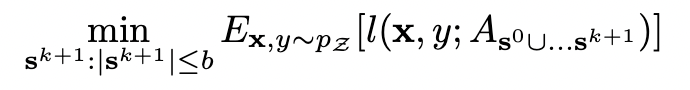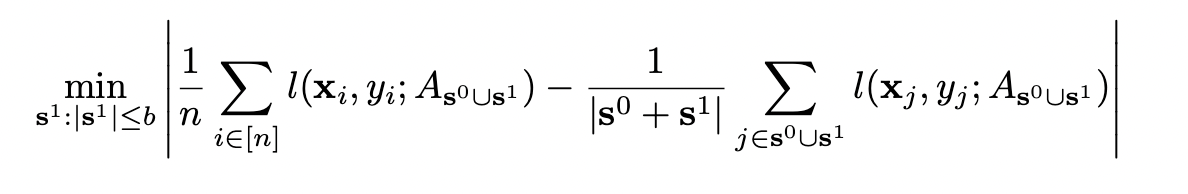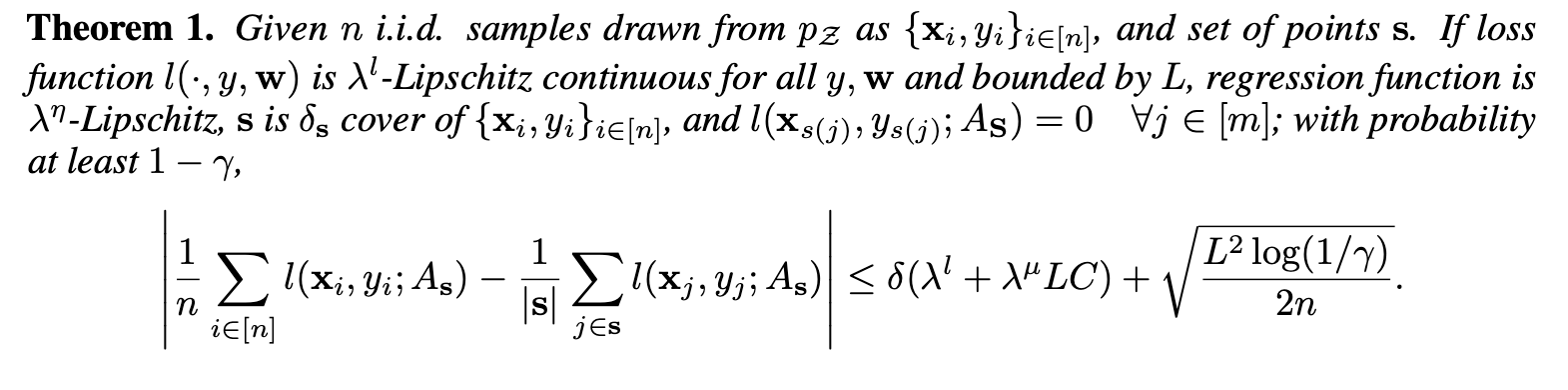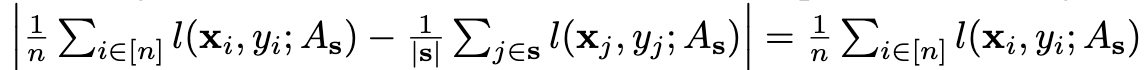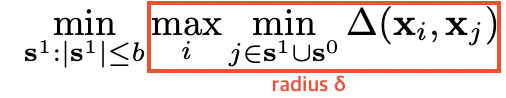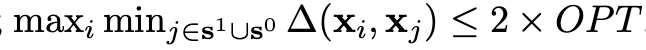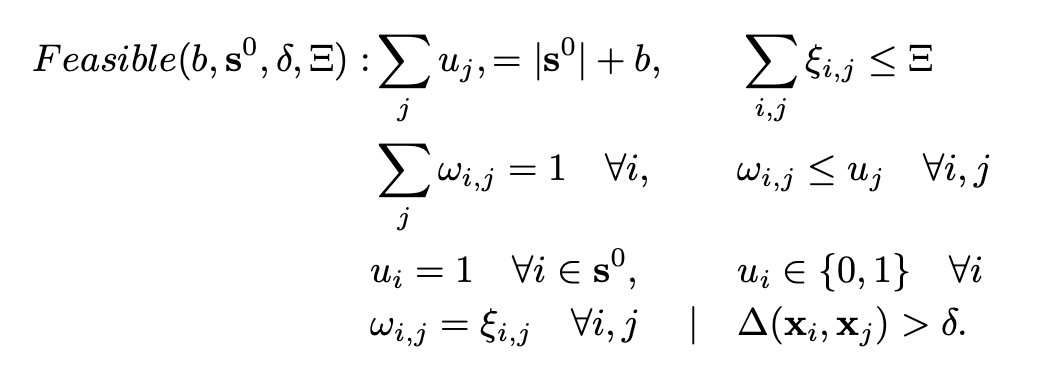📎 Paper: https://arxiv.org/abs/1708.00489
active learning에 대해 알아보며 읽었던 논문이다.
1. Introduction
- deep model을 학습시키려면 아주 많은 supervised examples로 이루어진 dataset이 필요하다.
- 하지만 이를 모으는 것은 time consuming & expensive 하다.
- 따라서 labeling 할 가치가 있는 image를 고르는 effective 한 방법(= active learning)이 필요하다.
- 하지만 기존의 active learning heuristics는 batch setting의 CNN에 적용하기에 적절하지 않다.
- 기존의 방법은 각 iteration에서 single point를 선택한다.
- single point는 local optimization 기법으로 인해 CNN에서 큰 영향을 미치지 못한다.
- 각 iteration은 convergence까지의 full training을 필요로 하기 때문에 label 하나하나를 query 하기 어렵다.
- 각 iteration에서 large subset의 label을 query 하는 방법이 필요하다.
- 기존의 방법은 각 iteration에서 single point를 선택한다.
- 따라서 active learning을 core-set selection 문제로 정의한다.
- 모든 data points를 이용하여 학습한 model 만큼의 성능을 낼 수 있도록 subset of points를 고르는 것이다.
- data points의 geometry를 이용하여 subset과 remaining points 간의 average loss의 bound를 minimize 한다. (== k-center problem)
- 이러한 방법은 image classification task에서 기존의 접근법들과 큰 차이로 outperform 하는 모습을 보였다.
2. Related Work
Active Learning
- 기존의 방법들은 large-scale datasets에 확장될 수 없어 batch sampling을 사용하는 large CNNs에 바로 적용할 수 없었다. (empirical analysis)
- information theoretical methods
- ensemble approaches
- uncertainty based methods (entropy, geometric distance to distance boundaries)
- Bayesian active learning (w/ dropout & approximate Bayesian inference)
- 최근에는 optimization based approaches가 등장했다.
- uncertainty와 diversity를 trade-off 하여, batch mode active learning setting에서 hard examples의 diverse set을 얻는 방법이다.
- 하지만 많은 양의 variables가 필요하여 마찬가지로 large-scale dataset에 확장될 수 없는 경우가 많다.
- 또한, pool based active learning algorithms도 등장했다.
- pool based on uncertainty 이면서, query 할 point를 고를 때에는 diversity를 이용하는 방법도 등장했다.
- 추가적인 기법을 통해 greedy active learning이 batch setting에서도 가능하다는 연구도 진행되었다.
- 본 논문에서 제시하는 방법은 uncertainty information을 전혀 사용하지 않고 diversity를 활용하는 discrete optimization based method에 속한다고 볼 수 있다.
Core-Set Selection
- 모든 data points를 이용하여 학습한 model 만큼의 성능을 낼 수 있도록 subset of points를 고르는 것이다.
- unsupervised subset selection algorithm과 비슷하며, dataset의 diverse cover를 찾는 문제이다.
Ladder Network
- 본 논문의 weakly-supervised learning 실험에서 사용하는 네트워크이다.
- supervised learning과 unsupervised learning 문제를 결합해서 해결하는 방식이다. (label이 있는 데이터와 없는 데이터를 모두 사용한다.)
- supervised cost function과 unsupervised cost function을 합쳐 동시에 minimize 한다.
기존 방법론과의 차별점
- active learning 문제를 core-set selection 문제로 정의했다.
- fully-supervised와 weakly-supervised 상황을 모두 고려했다.
- 다른 가정 없이 core-set selection 문제를 CNN에 직접 적용했다.
3. Problem Definition
- 참고 자료
notation
compact space $\mathcal X$ label space $\mathcal Y = \lbrace 1, …, C\rbrace $
($C$ classes classification problem)loss function $l(\cdot,\cdot ; \mathbf w):\mathcal X \times \mathcal Y \rightarrow \mathcal R$ query budget $b$ (oracle에게 label을 요청할 data의 개수) multiple rounds $k$ (query를 위해 선택된 subset: $\mathbf s^k$) classical 방법에서는 $b=1$ 이지만, single point는 deep learning에서 의미있는 영향이 없기 때문에 batch setting을 사용한다.
label이 되어야 할 data points의 initial pool은 uniformly random 하게 선정한다.
$n$ 전체 sample $m$ label $y$를 알고있는 sample $\lbrace\mathbf x_i\rbrace_{i \in [n]}$, $\lbrace y_{s(j)}\rbrace_{j \in [m]}$ active learning algorithm이 access 할 수 있는 정보
(initial sub-sampled pool의 labels 만 볼 수 있다.)$\mathbf s^0=\lbrace s^0(j)\in [n]\rbrace_{j \in [m]}$ initial labelled set 따라서 문제 정의를 다음과 같이 할 수 있다. (future expected loss를 minimize)
![first round]()
first round![multiple round]()
multiple round- active learning 알고리즘의 각 iteration에서 수행되는 두 단계는 다음과 같다.
- label을 query 할 data points의 set을 골라 oracle에게 query 한다.
- 새롭게 label을 얻은 것과 이전에 label을 얻은 data points에 대해서 classifier를 학습한다.
- fully-supervised 방법 - label 된 data만 가지고 학습한다.
- weakly-supervised 방법 - label 된 data와 아직 label이 되지 않은 data를 모두 학습에 사용한다.
4. Method
문제 재정의
minimize 하려는 loss는 다음의 항으로 이루어진다.
![Untitled]()
- generalization error - 이미 CNN에서는 무시 가능하다. (bounded)
- training error - CNN에서는 매우 낮다.
- core-set loss - active learning에서 critical 하다.
따라서 core-set loss를 이용한 다음의 식으로 active learning 문제를 재정의할 수 있다. 하지만 모든 label에 access를 할 수 없으므로 직접적으로 이를 계산할 수 없다. → upper bound를 이용하자!
![Untitled]()
Core-Set Loss는 Bounded 된 값이다.
minimize 하려는 loss function이 Lipschitz continuous 하다면, upper bound가 존재한다는 것을 증명했다.
![Untitled]()
training error는 0으로 간주하므로, core-set loss는 전체 dataset에 대한 average error와 같다.
![Untitled]()
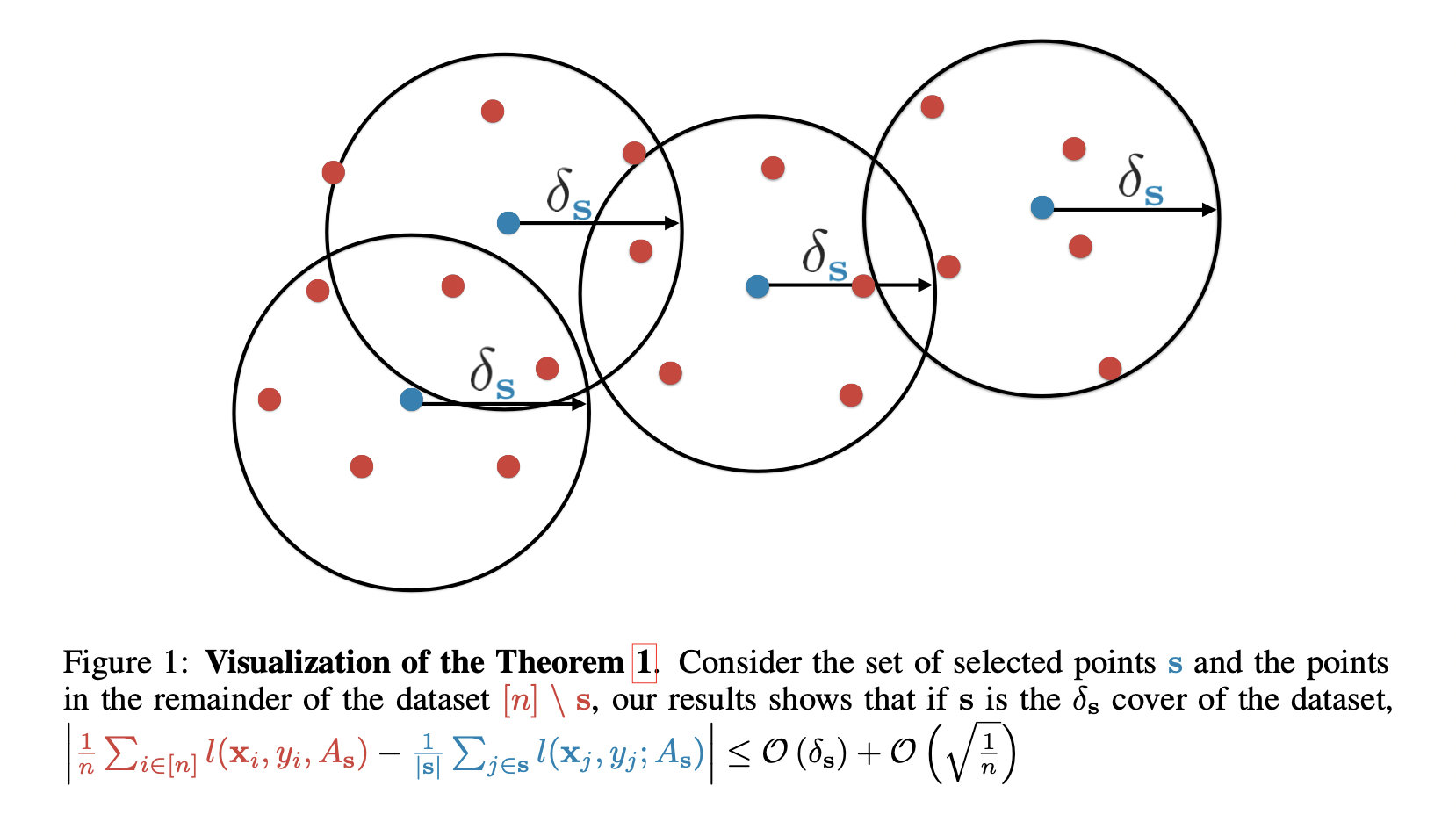
- upper bound는 covering radius $\delta$로 정의될 수 있다.
- set $\mathbf s$의 각 원소가 중심이고 radius가 $\delta$인 balls로 entire set $s^*$을 cover 할 수 있다.
- labelled points의 개수의 영향을 받지 않는다.
![Untitled]()
이 upper bound를 minimize 하자. ($\delta_s$와 관련)
\[\min_{\mathbf s^1: |\mathbf s^1 \le b|} \delta_{\mathbf s^0 \cup \mathbf s^1}\]
[Algorithm 1] K-Center-Greedy
- loss function의 upper bound를 minimize 하는 것 == k-Center problem
- 하나의 data point와 가장 가까운 center 사이의 최대 거리(== radius $\delta$)를 최소화하는 $b$ 개의 center points를 고르는 문제이다. 결과적으로 모든 data point를 cover 해야 한다.
NP-Hard 문제이지만 greedy approach를 이용한 2-OPT solution이 존재한다.
![Untitled]()
이렇게 구한 solution은 실제 optimal minimum의 2배보다 작거나 같다는 것이 증명되어 있다.
![Untitled]()
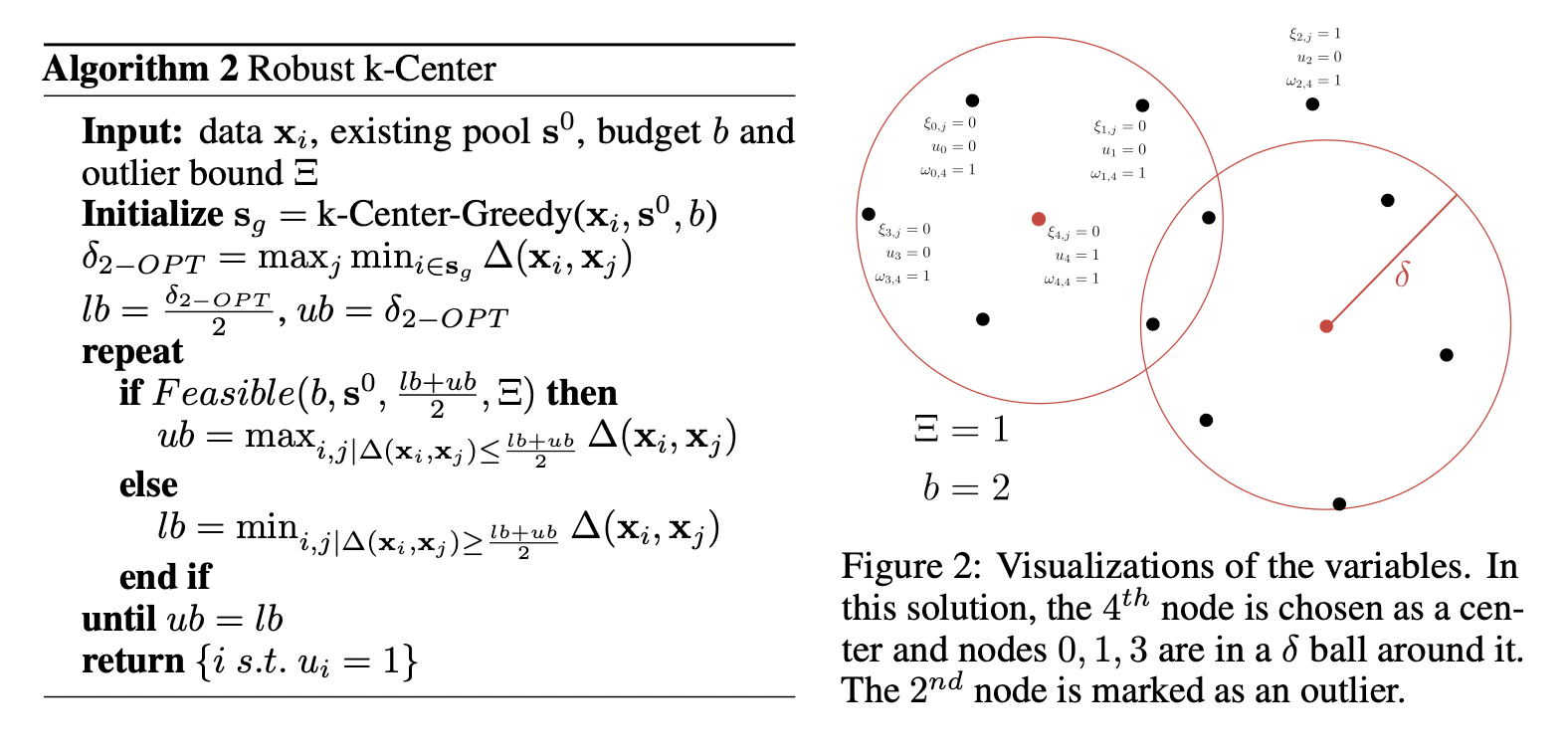
[Algorithm 2] Robust K-Center
- [Algorithm 1] k-Center-Greedy를 initialization으로 사용한 후, MIP의 feasibility를 반복적으로 확인하는 방법이다.
- $OPT \le \delta$ → mixed integer program(MIP)으로 정의한다.
- outliers의 개수의 upper limit $\Xi$(= cover 하지 않을 sample 수)을 도입하여 robustness를 개선한다.
$\delta$가 얼마가 되었을 때 제약식을 모두 만족시키는지 알 수 없으므로, lower / upper bound를 설정 후 업데이트를 계속 하면서 그 두 값이 같아질 때의 set이 optimal solution이라고 판단한다.
![Untitled]()
- $\delta$ 값을 계속 바꿔가면서 MIP가 언제 feasible($\min_{\mathbf s^1}\max_{i}\min_{j\in \mathbf s^1 \cup \mathbf s^0}\Delta(\mathbf x_i, \mathbf x_j)\le\delta$) 한지 확인한다.
다음의 값은 모두 0 또는 1이다.
$u_i$ i-th data pointer가 center로 선택되면 1 $\mathcal w_{i,j}$ i-th point가 j-th point로 covered 되면 1 $\xi_{i,j}$ i-th point가 outlier이면서 $\delta$ constraint 없이 j-th point에 의해 covered 되면 1
Implementation Details
| distance | final fully-connected layer에서 나온 activations의 L2 distance |
| network | (CNN) VGG-16 (weakly-supervised learning) Ladder networks |
| upper bound on outliers $\Xi$ | 1e-4 * n (n: unlabelled points의 개수) |
| etc | He initialization, RMSProp(lr=1e-3), Gurobi (MIP framework) |
5. Experimental Results
Task & Dataset
- image & digit classification task
- CIFAR-10, CIFAR-100, SVHN
Results
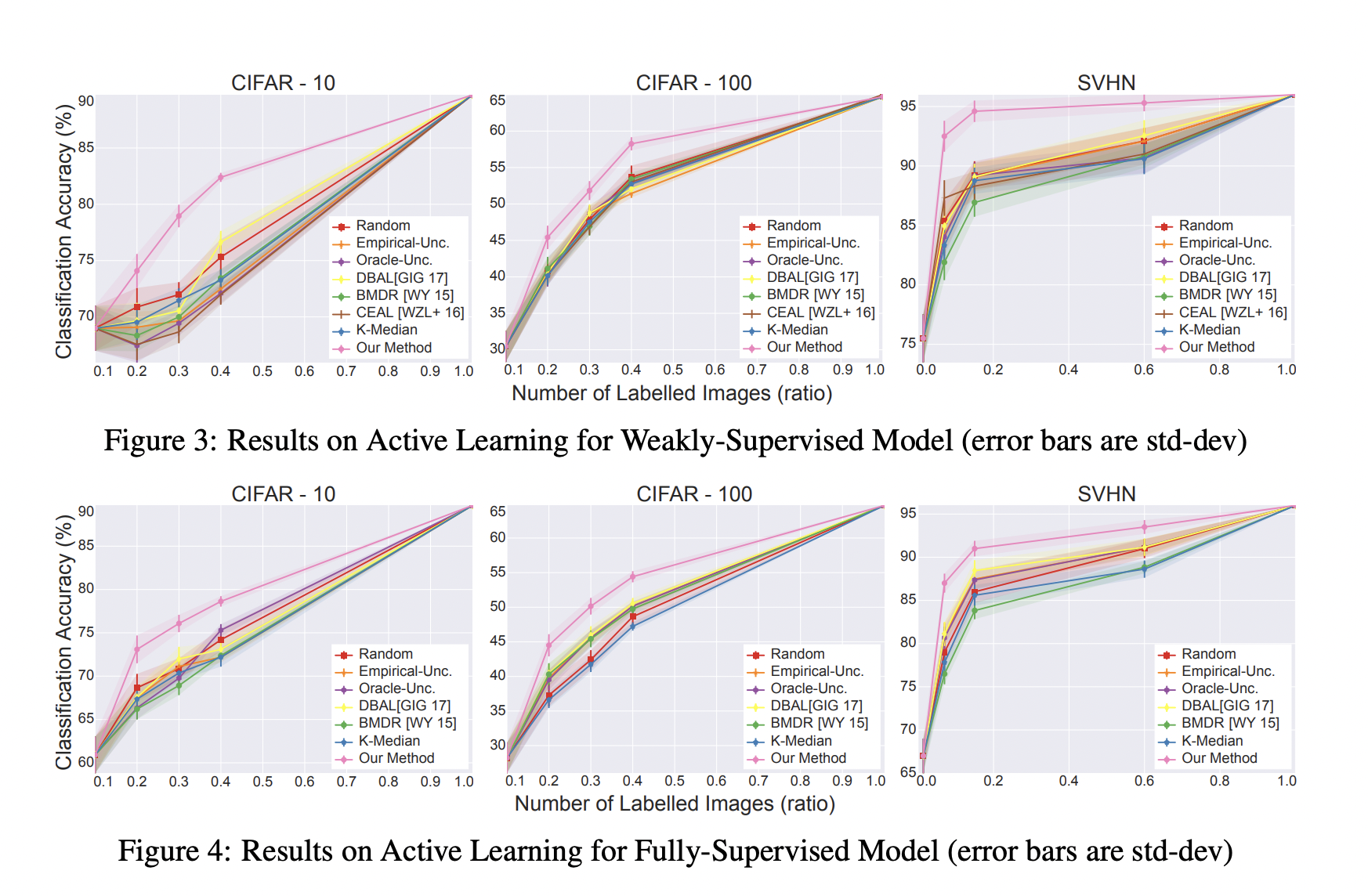
- 모든 실험에서 our algorithm이 모든 baseline에 비해 성능이 뛰어났다.
- 특히, weakly-supervised model에서 성능이 크게 뛰어났다. (geometric method → better feature learning)
- CIFAR-100 데이터셋에서 상승 폭이 상대적으로 작았다. (core-set loss의 bound가 class 개수에 영향을 받으므로)
- 기존의 batch mode active learning baseline 방법들이 무조건 greedy baseline 방법들보다 성능이 좋은 것은 아니었다.
- 여전히 uncertainty information을 사용하기 때문이다.
- soft-max probability가 uncertainty의 좋은 proxy가 아니기 때문이다.
- batch setting에서는 uncertainty를 이용한 방법보다 오히려 random sampling이 성능이 좋은 경우가 많다.
- uncertainty를 이용한 방법은 space의 큰 비율을 cover 하지 못하기 때문이다. 이에 반해 our algorithm은 전체 space에서 골고루 query 한다.
![Untitled]()
Optimality
- our algorithm = [initialization] greedy 2-OPT solution + [iteration] check feasibility of MIP
- MIP의 average run-time을 측정한 결과, dataset of 50k images에 대해서는 합리적인 시간 안에 converge가 가능하다는 것을 알 수 있었다.
따라서 our algorithm도 실제로 적용 가능한 수준의 run-time이 소요된다.
![Untitled]()
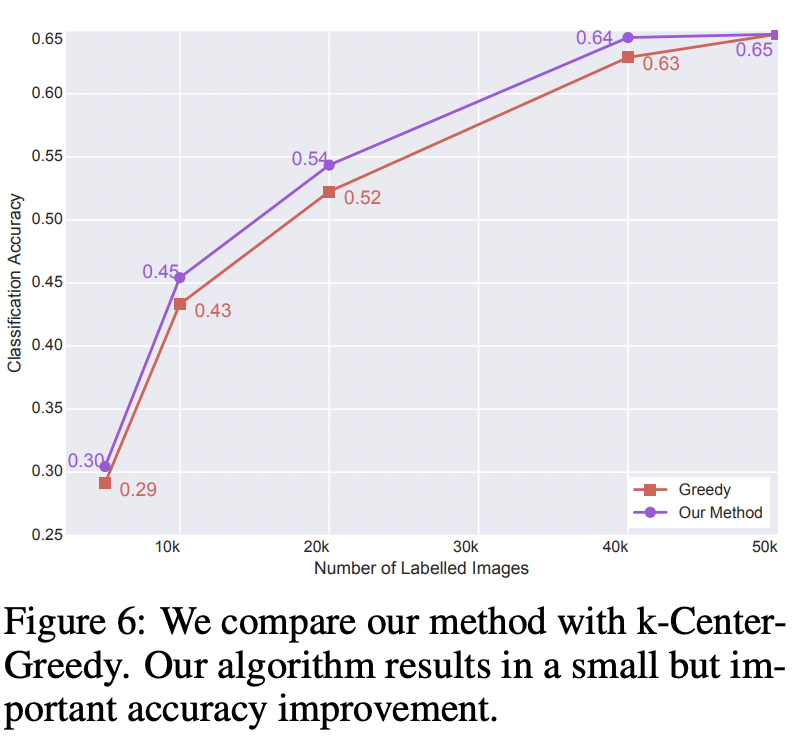
- k-Center-Greedy와 our method의 accuracy를 비교한 결과, 약간의 성능 향상이 있었다.
dataset의 크기가 너무 커서 MIP가 feasible 하지 않아 2-OPT solution만을 이용하더라도, 다른 baseline에 비해 성능이 좋다.
![Untitled]()
6. Conclusion
- active learning의 classical uncertainty based methods는 batch sampling으로 인한 correlation 때문에 CNN에 적용이 제한적이었다.
- active learning 문제를 core-set selection 문제로 재정의한 결과, 큰 성능 향상을 확인할 수 있었다.