[Paper] ArcFace: Additive Angular Margin Loss for Deep Face Recognition

📎 Paper: https://arxiv.org/abs/1801.07698

당시 face recognition 분야에서 class separability를 최대화 하기 위해 softmax loss function에 margins를 adopt 하는 방식이 연구되고 있었다. 본 논문에서는 Additive Angular Margin Loss (ArcFace)를 제안하며, label noise에 강한 sub-center ArcFace도 제안한다. 또한, inverse problem인 feature vector를 face image로 mapping 하는 문제에도 적용 가능함을 보여준다.

1. Introduction

1.1 Recent Studies

face recognition 관련 연구의 큰 두 줄기는 다음과 같다.

1. multi-class classifier를 학습한다. (ex. softmax classificer)
2. embedding을 학습한다. (ex. triplet loss)

하지만 해당 방법들의 단점은 다음과 같다.

1. softmax loss
   • open-set face recognition 문제에서 discriminative 하지 못하다.
   • linear transformation matrix의 크기가 identities의 수에 따라 선형적으로 증가한다.
2. triplet loss
   • large-scale dataset에 대해서 triplets의 개수가 폭발적으로 늘어난다.
   • semi-hard sample mining이 어렵다.

margin benefit을 채택하면서도 triplet loss에서의 sampling problem을 피하기 위해서 최근에는 margin penalty를 more feasible framework(ex. softmax loss)에 통합하는 방법이 시도되고 있다.

• embedding feature와 linear transformation matrix 간의 multiplication step에서 global sample-to-class comparisons가 이루어진다.
• linear transformation matrix의 각 column은 특정 class를 대표하는 class center로 볼 수 있다.

Sphereface는 angular margin을 도입했으며, unstable training을 보완하기 위해 hybrid loss(standard softmax loss 포함)를 제안했다. 하지만 이는 softmax loss가 training process를 dominate 하게 된다.

1.2 ArcFace

본 논문에서는 training process를 stabilize하고 face recognition에서 discriminative power를 개선하기 위한 Additive Angular Margin loss를 제안한다.

• DCNN feature와 last fully connected layer 간의 dot product = cosine distance (after feature and center normalization)
• arc-cosine function을 통해 current feature와 target center 간의 angle을 계산한다.
• normalized hypersphere에서의 angle과 arc의 exact correspondence로 인해 직접적으로 geodesic distance margin을 최적화할 수 있다. → “ArcFace”

1.3 Sub-Center ArcFace

margin-based softmax methods가 큰 성능 향상을 이루어냈으나, 모두 well-annotated clean dataset에 대해서 학습되어야 했다. 따라서 real-world의 massive noisy data에 대해 robustness를 향상시키는 방법이 필요했다. → “sub-center ArcFace”

• 모든 samples가 대응되는 positive centers에 가깝도록 하는 intra-class constraint를 도입하는 방법이다. 즉, 각 class 마다 K sub-centers가 존재하며, training sample이 오직 그 K positive sub-centers 중 하나에만 가까우면 된다.
• ArcFace의 경우, noisy sample이 large wrong loss value를 생성하여 학습을 방해하지만, sub-center ArcFace의 경우 intra-class constraint로 인해 training sample이 multiple positive sub-centers 중 하나에 가깝도록 강제한다.

• sub-center ArcFace에서 noise는 non-dominant sub-class를 형성하게 된다.

  one dominant sub-class	majority clean faces를 포함한다.
  multiple non-dominant sub-classes	hard, noisy faces를 포함한다.

• 따라서 non-dominant sub-centers와 high-confident noisy samples를 drop 함으로써 자동으로 large-scale clean training data를 얻을 수 있다.

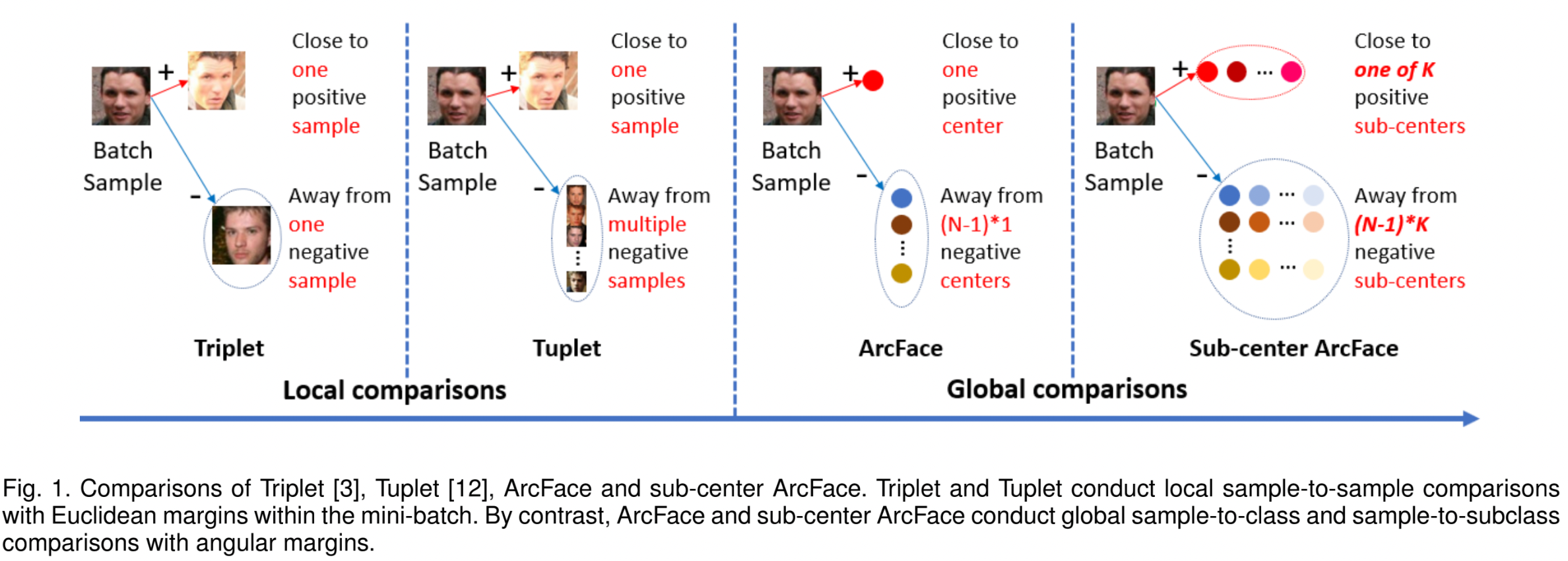
1.4 Comparison to Other Methods

Local Comparisons

• triplet loss: mini-batch 안에서, Euclidean margin을 이용한 local sample-to-sample 비교
• tuplet loss: mini-batch 내의 모든 negative pairs를 이용한 비교

Global Comparisons

• ArcFace: angular margin을 이용한 global sample-to-class 비교
• sub-center ArcFace: angular margin을 이용한 global sample-to-subclass 비교

1.5 Inverse Problem

• ArcFace는 low-dimensinal latent space를 highly nonlinear face space로 mapping 하는 문제에도 적용될 수 있다.
• pre-trained ArcFace model은 추가적인 generator나 discriminator의 학습 없이, gradient와 statistic prior(BN layers에 저장된 mean과 variance)만 사용해서 identity-preserved & visually reasonable한 face images를 생성할 수 있다.

1.6 Advantages of ArcFace

1. intuitive
   • 직접적으로 geodesic distance margin을 optimize 한다. (normalized hypersphere에서 angle과 arc 간의 exact correspondence 덕분)
   • additive angular margin loss로 인해 intra-class compactness와 itner-class discrepancy를 향상시킬 수 있다.
2. economical
   • sub-class를 도입하여 massive real-world noises에 대해 robustness를 개선할 수 있다.
   • sub-center ArcFace를 통해 자동으로 large-scale raw web faces를 cleaning 할 수 있다.
3. easy
   • 기존의 여러 deep learning frameworks로 쉽게 구현 가능하다.
   • stable convergence를 위해 다른 loss functions와 결합될 필요가 없다.
4. efficient
   • training 시 무시할만한 computational complexity 만을 추가한다.
5. effective
   • face recognition benchmarks에서 state-of-the-art performance를 달성했다. (large-scale image and video datasets)
6. engaging
   • discriminative power 뿐만 아니라 generative power도 가진다.
   • gradient와 BN layer의 statistic priors를 이용하여 identity-preserved & visually plausible face images를 restore 할 수 있다.

---

2. Related Work

2.1 Face Recognition with Margin Penalty

• Triplet Loss
  • Euclidean distance margin을 사용한다.
  • mini-batch 내에서 sample-to-sample comparisons를 수행한다. (local)
  • large-scale dataset에서는 combinatorial explosion이 발생하며, informative mini-batch를 선택하고 representative triplets를 고르는 effective sampling strategies가 필요하다는 단점이 있다.
• Margin-based softmax methods
  • feasible framework에 margin penalty를 통합하는 방식으로, sample-to-class comparisons를 수행한다. (global)
  • sample-to-class comparison이 sample-to-sample comparison보다 efficient & stable 하다.
    1. class 개수가 sample 개수보다 훨씬 적기 때문이다.
    2. 각 class는 online으로 update 될 수 있는 smoothed center vector로 나타낼 수 있기 때문이다.

2.2 Face Recognition under Noise

대부분의 face recognition dataset은 인터넷에서 다운받은 데이터로, massive noisy data이다. 따라서 이를 해결하기 위한 연구들이 진행되어 왔다.

2.3 Face Recognition with Sub-classes

subclass division은 different face modalities(ex. frontal view, side view)에 적용할 수 있다. 이는 face recognition의 성능을 향상시킨다.

2.4 Face Synthesis by Model Inversion

• GAN을 중심으로 identity-preserving face generation 관련 연구가 진행되어 왔으나, generator를 학습시킬 때 original data에 접근이 필요하게 되어 data privacy 문제가 발생할 수 있다.
• 따라서 single CNN을 통해 image synthesis를 수행하는 model inversion이 연구되었다.
• generative face recognition model
  • mean face와 특정 face가 얼마나 다른지를 계산하는 방법인 Eigenface가 있다.
  • 최근에는 BN layers에 저장된 statistics(ex. mean, variance)를 이용한 data-free method가 제안되었다.

---

3. Proposed Approach

3.1 ArcFace

Modification of Softmax

기존의 softmax loss는 intra-class samples 간에 higher similarity / inter-class samples 간에 diversity를 enfore 하지 못한다.

\[L_1=-\log\frac{e^{W_{y_i}^Tx_i+b_{y_i}}}{\sum_{j=1}^N e^{W_j^T x_i+b_j}}\]

\[L_3=-\log \frac{e^{s\cos(\theta_{y_i}+m)}}{e^{s\cos(\theta_{y_i}+m)}+\sum_{j=1, j\ne y_i}^N e^{s\cos\theta_j}}\]

• logit을 $W_j^Tx_i=|W_j||x_i|\cos\theta_j$ 로 변경한다.
  • $\theta_j$ = weight $W_j$와 feature $x_i$ 간의 각도
  • $|W_j|=1$로 고정 (L2 normalization)
  • $|x_i|$ = L2 normalization → re-scale to $s$ (= radius of hypersphere)
  • prediction이 feature와 weight 간의 각도에만 의존하도록 한다.

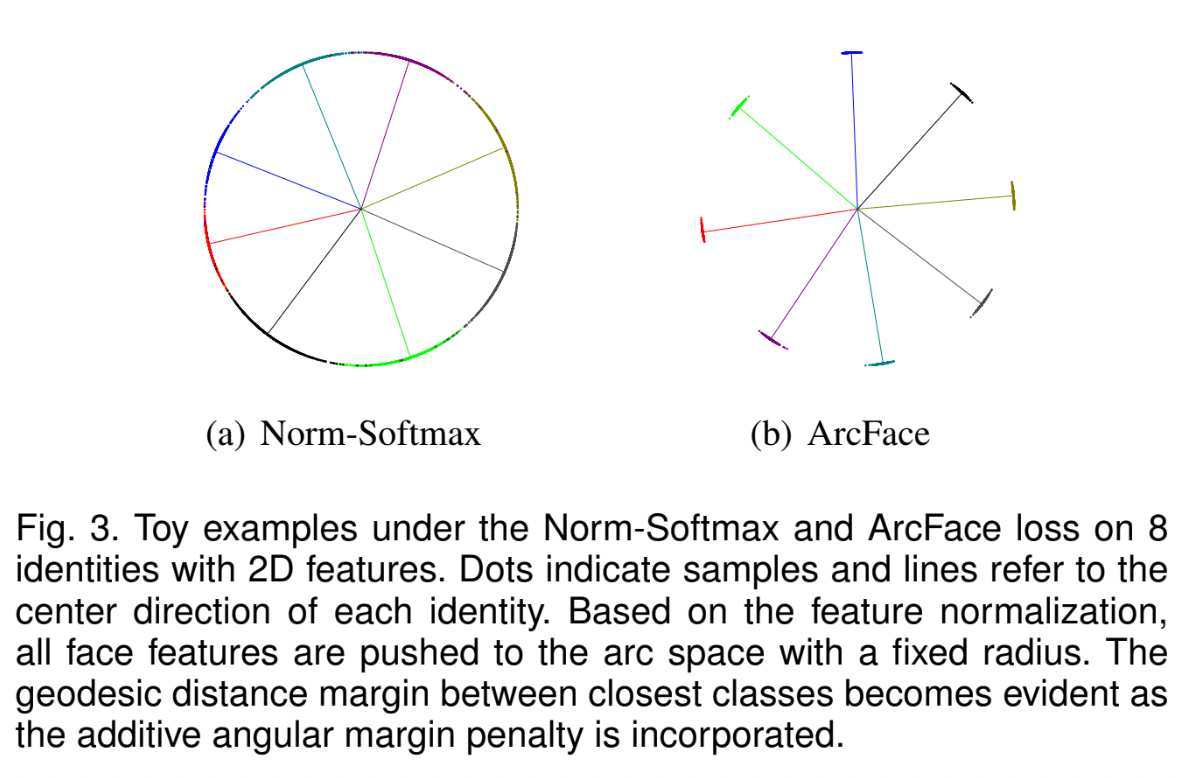
• embedding feautres가 hypersphere 위의 각 feature center 주변에 분포하게 되므로, $x_i$와 $W_{y_i}$ 사이에 additive angular margin penalty $m$을 부여하여 intra-class compactness와 inter-class discrepancy를 향상시킨다.

  additive angular margin penalty

  == geodesic distance margin penalty in the normalized hypershpere

  → “ArcFace”

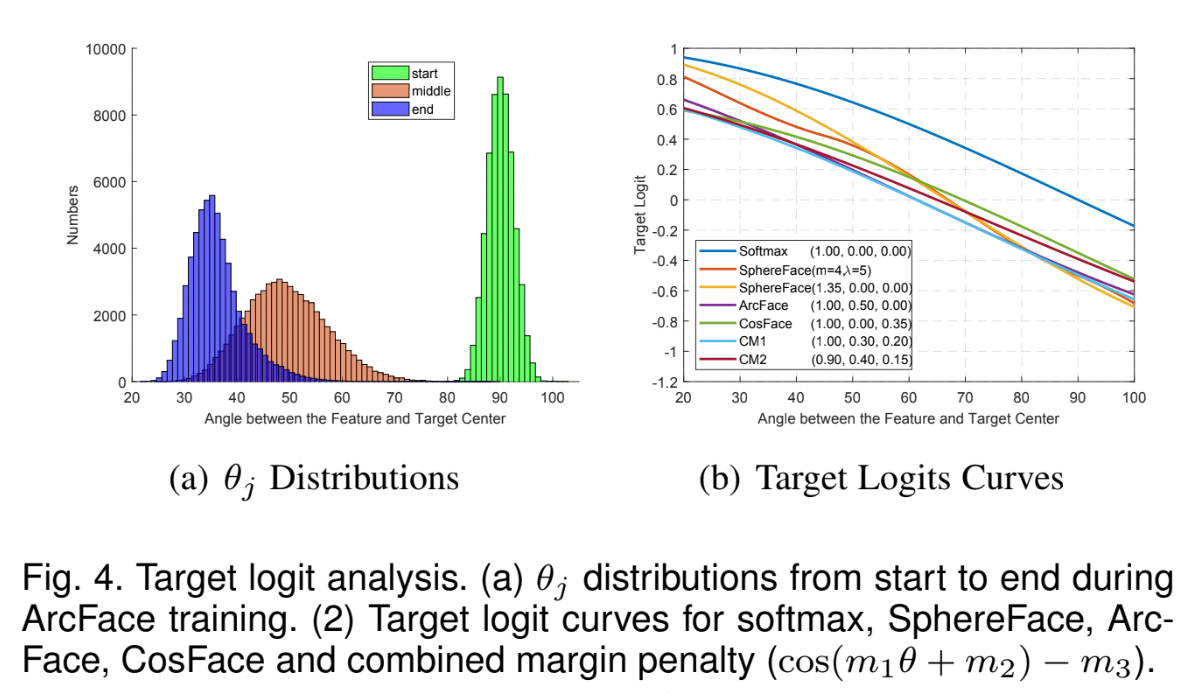
Margin Penalty 방법 간 비교

모든 method를 하나의 통합된 framework로 나타내면 다음과 같다.

• SphereFace = multiplicative angular margin $m_1$
• ArcFace = additive angular margin $m_2$
• CosFace = additive cosine margin $m_3$

\[L_4=-\log \frac{e^{s\cos(m_1\theta_{y_i}+m_2)-m_3}}{e^{s\cos(m_1\theta_{y_i}+m_2)-m_3}+\sum_{j=1, j\ne y_i}^N e^{s\cos\theta_j}}\]

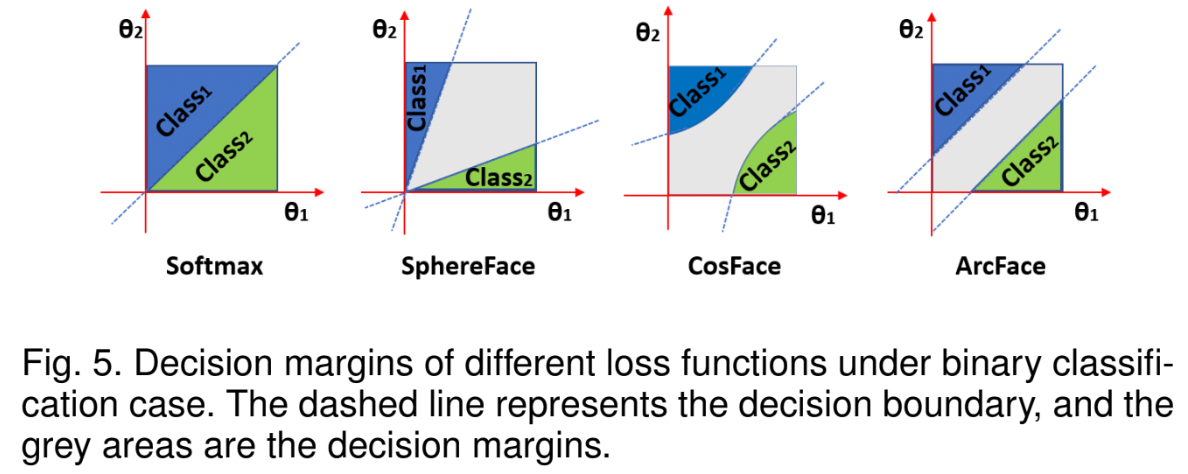
Geometric Difference

• additive angular margin은 geodesic distance와 정확히 대응되어 더 나은 geometric attribute를 가지고 있다.
• binary classification case에서의 decision boundaries
  • ArcFace = constant linear angular margin
  • SphereFace, CosFace = nonlinear angular margin

  

Other Intra and Inter Losses

$L_2$

\[L_2=-\log \frac{e^{s\cos\theta_{y_i}}}{e^{s\cos\theta_{y_i}}+\sum_{j=1, j\ne y_i}^N e^{s\cos\theta_j}}\]

• intra-loss: sample - ground truth center 간의 angle/arc를 감소시켜 intra-class compactness를 개선하기 위한 것이다.

  \[L_5=L_2+\frac{1}{\pi}\theta_{y_i}\]

• inter-loss: 다른 centers간 angle/arc를 증가시켜 inter-class discrepancy를 향상시키기 위한 것이다.

  \[L_6=L_2-\frac{1}{\pi(N-1)}\sum_{j=1, j\ne y_i}^N \arccos(W_y^T, W_j)\]

• 다음과 같이 angular representation에 triplet loss를 적용한다.

  \[\arccos (x_i^{pos}, x_i)+m \le \arccos(x_i^{neg}, x_i)\]

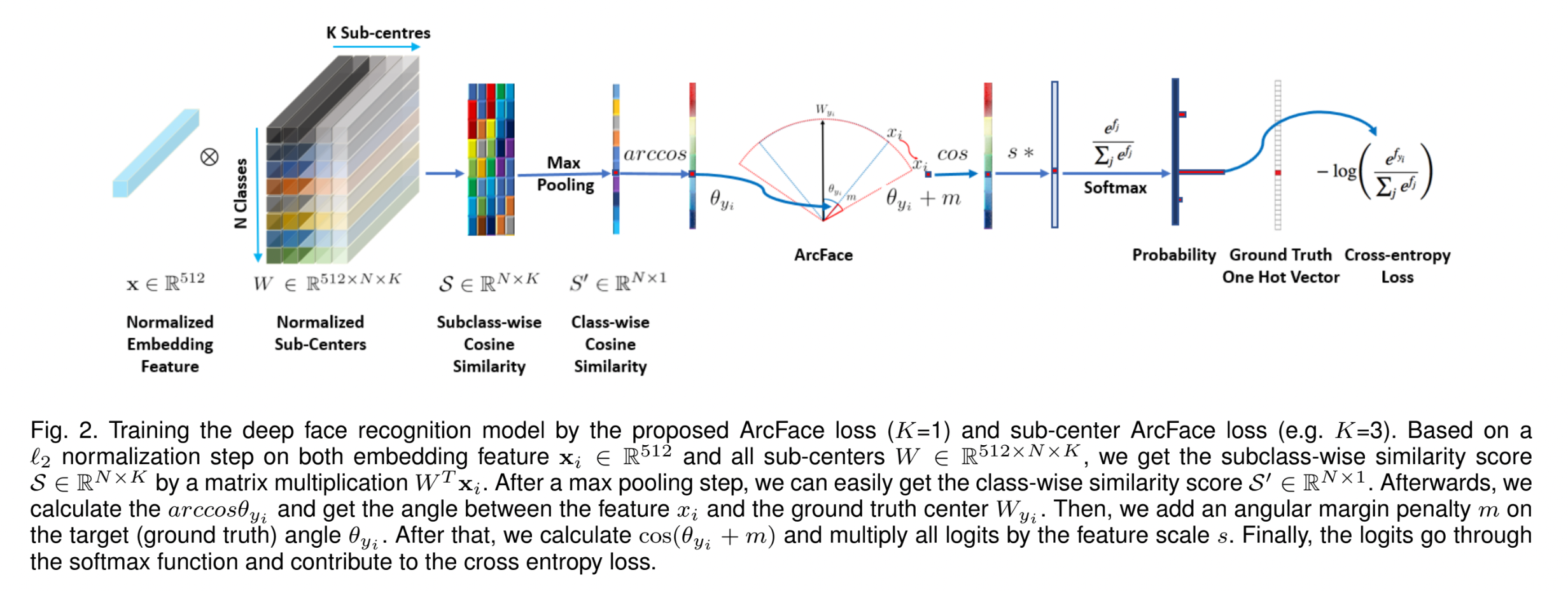
3.2 Sub-center ArcFace

• 각 identity 마다 sub-class를 사용하여 noise에 robust 해지도록 한다.
  • 각 identity에 대해 $K$ sub-centers를 설정한다.
  • embedding features: $\mathbf x_i \in \mathbb R^{512}$
  • all sub-centers: $W \in \mathbb R^{512\times N\times K}$
  • subclass-wise similarity scores: $\mathcal S \in \mathbb R^{N\times K}$ (by matrix multiplication $W^T\mathbf x_i$)
  • class-wise similarity score (by max pooling $\mathcal S$): $\mathcal S’ \in \mathbb R^{N\times 1}$

• Sub-center ArcFace loss

  \[L_7 =-\log \frac{e^{s\cos(\theta_{y_i}+m)}}{e^{s\cos(\theta_{y_i}+m)}+\sum_{j=1, j\ne y_i}^N e^{s\cos\theta_j}}\] \[\theta_j=\arccos (\max_k(W_{j_k}^T\mathbf x_i)), k\in \{1, ..., K\}\]

Dropping High-Confident Noisy Data

자동으로 faces를 cluster 하여 hard / noisy samples가 dominant clean samples로부터 분리되도록 할 수 있다.

• 일부 noisy samples는 그들의 centers로부터 멀리 떨어져 있다.
• hard threshold(ex. angle $\ge 77^{\circ}$ or cosine $\le 0.225$)를 주어 noisy tail를 제거할 수 있다.

• samples의 4가지 분류
  • easy clean samples: dominant sub-classes로부터 나온 samples
  • hard noisy samples: dominant sub-classes로부터 나온 samples
  • hard clean samples: non-dominant sub-classes로부터 나온 samples
  • easy noisy samples: non-dominant sub-classes로부터 나온 samples
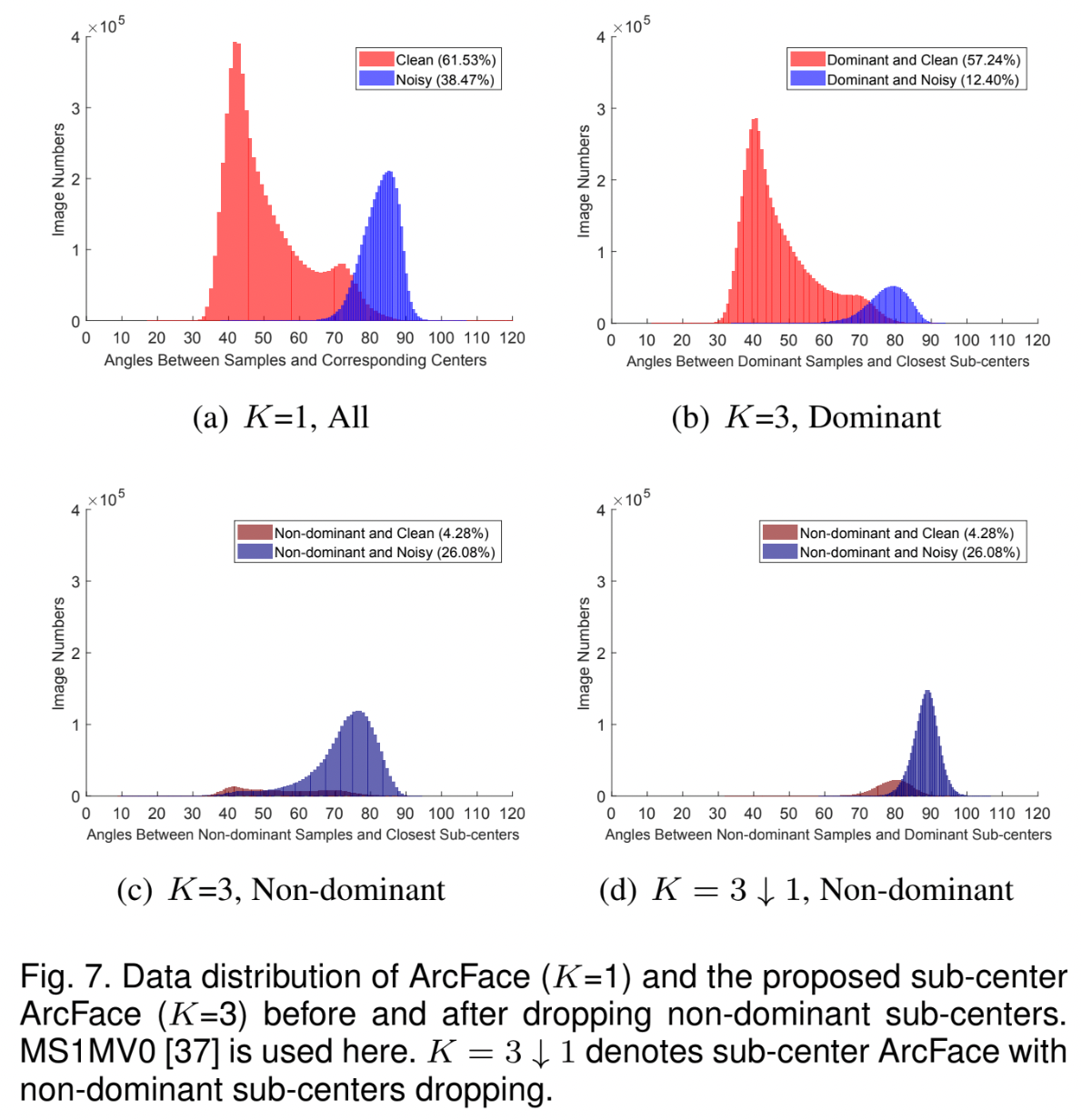
• sub-center ArcFace를 통해 noise rate를 1/3 가량 감소시킬 수 있다. (38.47% → 12.40%)
• Figure 7(b)와 7(d)를 통해 high-confident noisy samples를 drop 하기 위한 constant angle threshold($70^{\circ}$ 와 $80^{\circ}$ 사이)를 찾을 수 있다.
• 이처럼 high-confident noisy data를 drop한 이후, automatically cleaned dataset에서 ArcFace model을 retrain from scratch 한다.

3.3 Inversion of ArcFace

pre-trained ArcFace model을 통해 identity preserved & visually plausible face images를 얻을 수 있다. 이때, 다음의 정보만을 이용한다.

• ArcFace Loss의 gradient

• BN layers에 저장된 face statistic priors (ex. mean, variance)

  \[L_8=\sum_{i=0}^L\|\tilde \mu_i^r-\mu_i\|_2+\|\tilde \sigma_i^r-\sigma\|_2^2\]
  • $\mu_i^r/\sigma_i^r$: layer $i$에서의 분포에 대한 mean / standard deviation
  • pre-trained ArcFace의 $i$-th BN layer에 각각에 대응되는 parameters가 저장되어 있다.

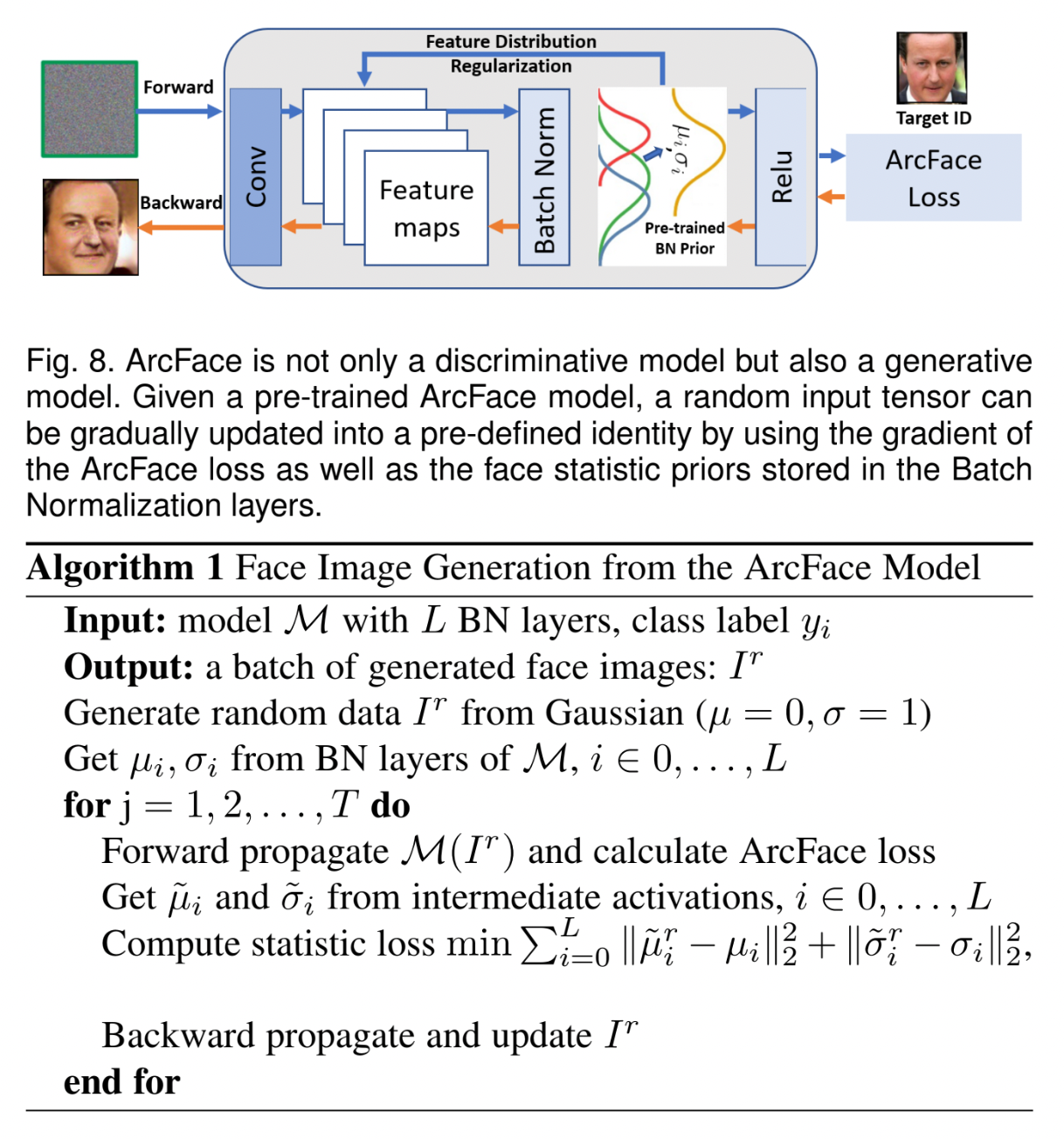
Algorithm

Algorithm 1에서처럼 $L_3+\lambda L_8, \lambda=0.05$ 를 $T$ steps에 걸쳐 optimize 한 후, pre-defined identity와 동일한 identity이며 original dataset의 statistical distribution과 비슷한 faces를 생성할 수 있다.

Open-Set Face Generation

embedding feature로부터 open-set face generation을 해결하기 위해 feature pairs 간의 classification loss를 L2 loss로 대체한다.

• open-set face generation

  restore the face image from any embedding feature

• close-set face generation

  reconstructs face images from the class centers stored in the linear weight

---

4. Experiments

4.1 Implementation Details

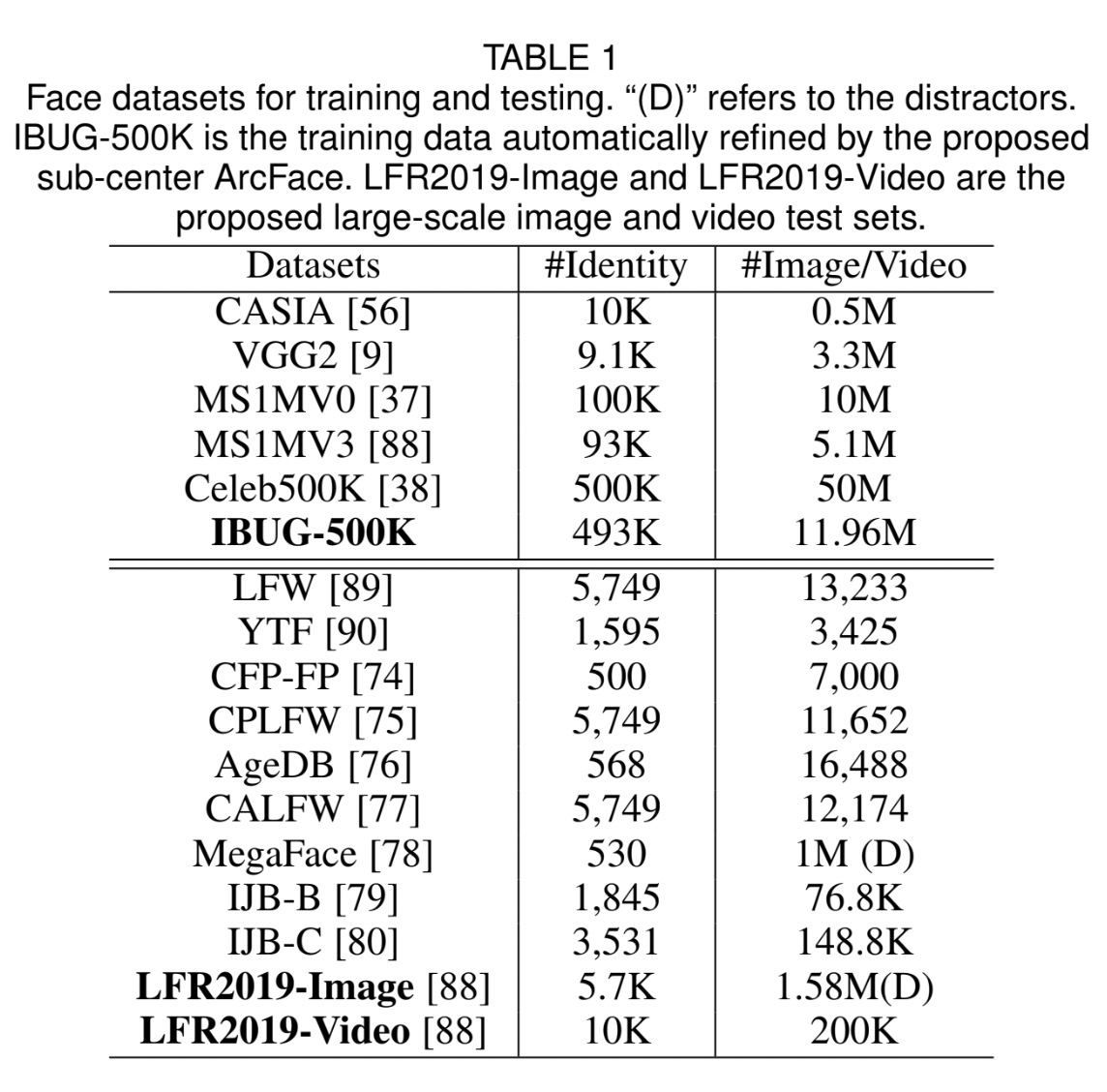
Dataset

Experimental Settings

• ArcFace
  • RetinaFace를 통해 normalized face crops (112x112)를 생성한다.
  • embedding network로는 ResNet50, ResNet100(w/o bottleneck structure)을 사용하며, 최종적으로 512-D embedding feature를 얻는다.
  • feature scale $s$ = 64, angular margin $m$ = 0.5
  • 자세한 내용은 논문 참고
• Sub-center ArcFace
  • first round model에 대해 다음을 drop 한다.
    • non-dominant sub-centers ($K=3\downarrow 1$)
    • high-confident noisy data ($> 75^{\circ}$)
  • 그 후, cleaned data를 가지고 retrain from scratch 한다.

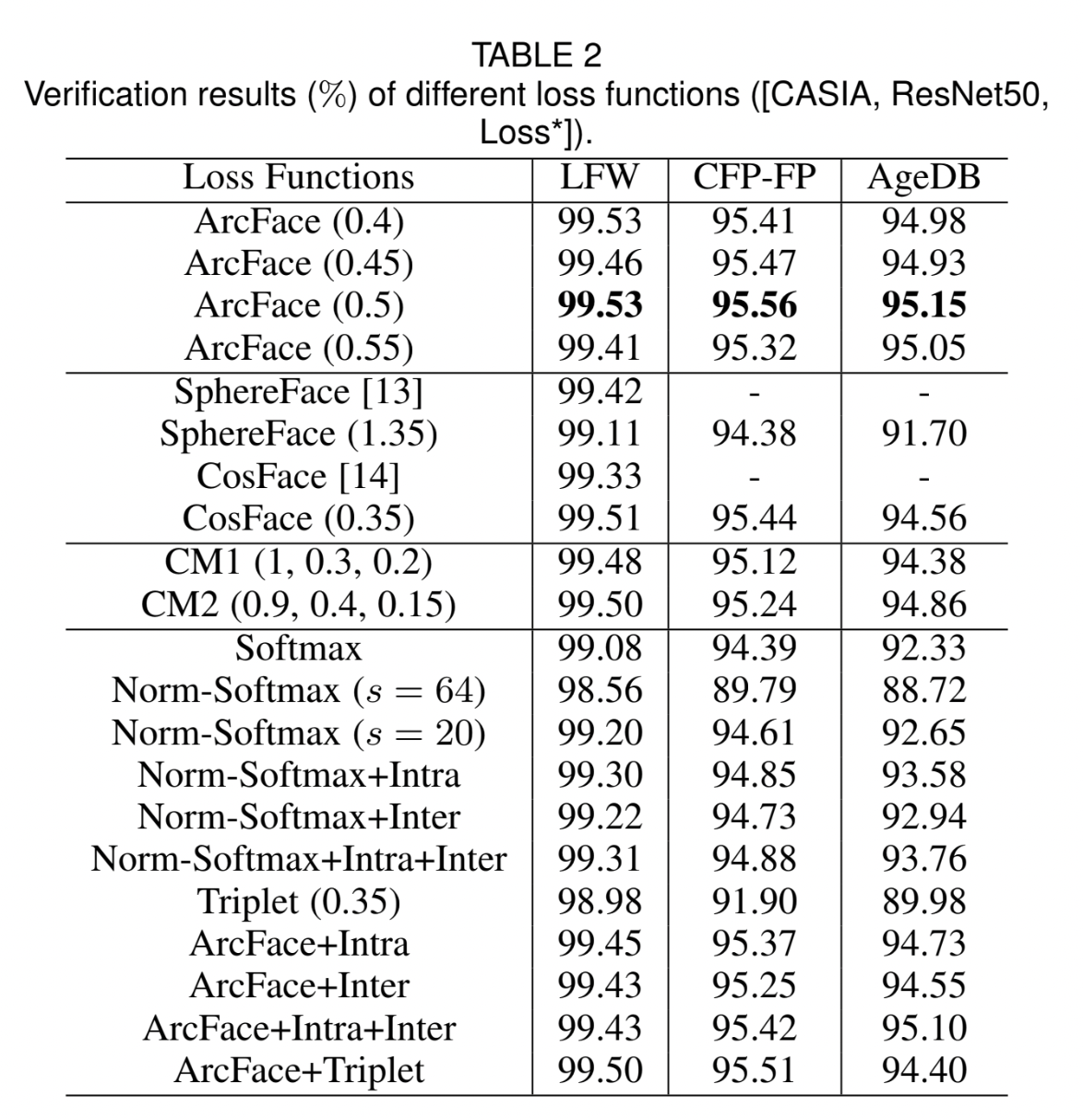
4.2 Ablation Study on ArcFace

ArcFace가 모든 3개의 test sets에서 highest verification accuracy를 달성했다.

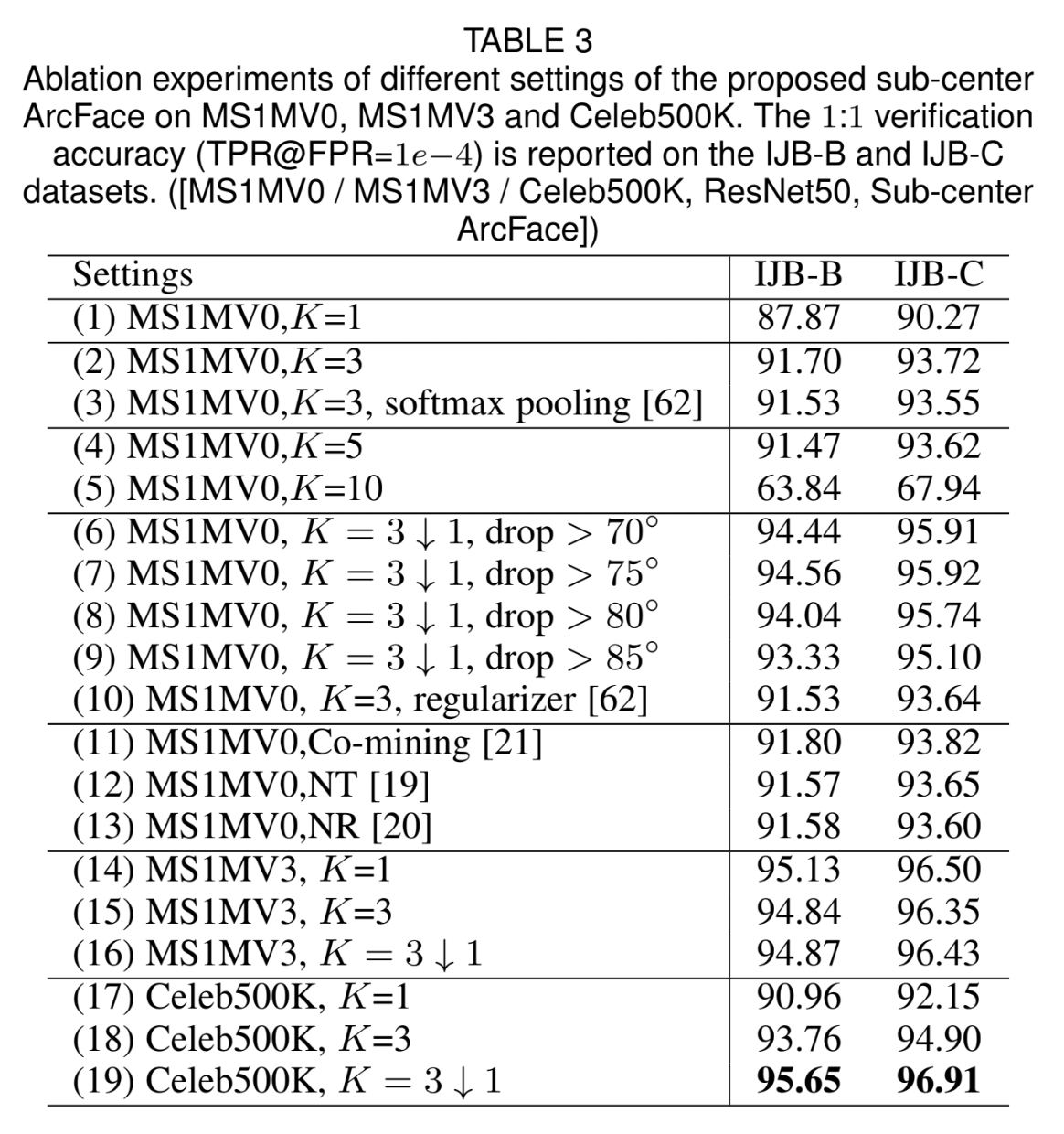
4.3 Ablation Study on Sub-center ArcFace

noisy training dataset에 대해 sub-center ArcFace를 적용해보았다.

• ArcFace는 noisy dataset에서 performance drop(96.50% → 90.27%)이 있는 반면, sub-center ArcFace는 더 robust(93.72%) 했다.
• 너무 많은 sub-centers(= too large $K$)는 intra-class compactness를 약화시켜 accuracy를 크게 떨어뜨릴 수 있다. noise tolerance와 intra-class compactness 간 balance를 잘 유지해야 하며, 본 논문에서는 $K=3$을 선택했다.
• nearest sub-center assignment 시 max pooling을 사용할 때가 softmax pooling을 사용할 때보다 성능이 살짝 더 좋았다. (93.72% vs. 93.55%)
• non-dominant sub-centers와 high-confident noisy samples를 drop 하는 것을 통해 regularization을 추가하는 것보다 더 좋은 성능을 낼 수 있다. (95.92% vs. 93.64%)
• constant threshold에 크게 sensitive 하지 않으며(95.91% vs. 95.92% vs. 95.74%), 본 실험에서는 high-confident noisy samples를 drop 하기 위한 threshold로 $75^{\circ}$를 선택했다.
• co-mining, re-weighting 등의 방법들보다 ArcFace가 automatic clean & noisy data isolation에 더 효과적이다.
• noisy dataset에 대해 학습한 sub-center ArcFace는 manually cleaned dataset에 대해 학습한 ArcFace와 비슷한 수준의 성능을 보였다. (95.92% vs. 96.50%)

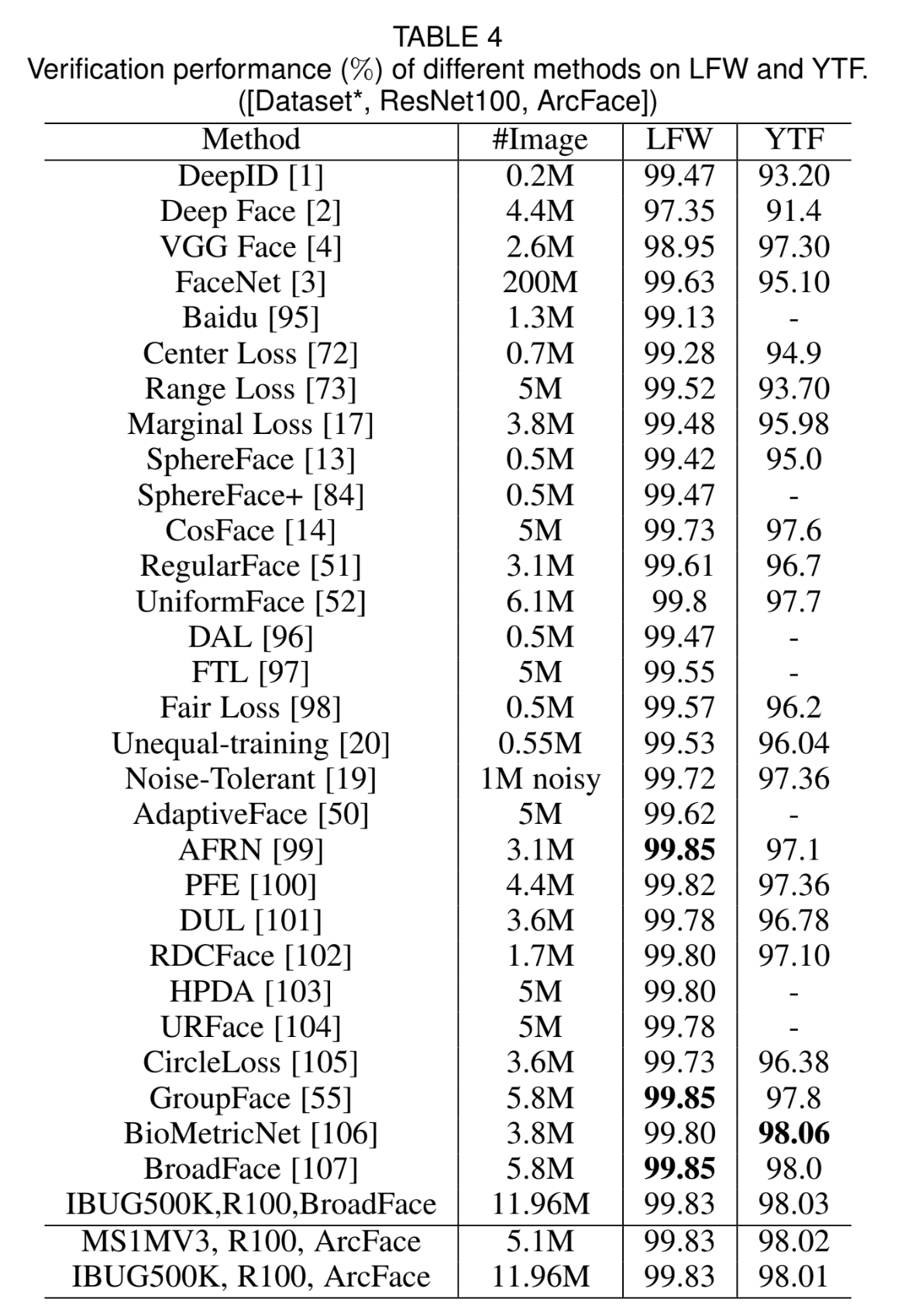
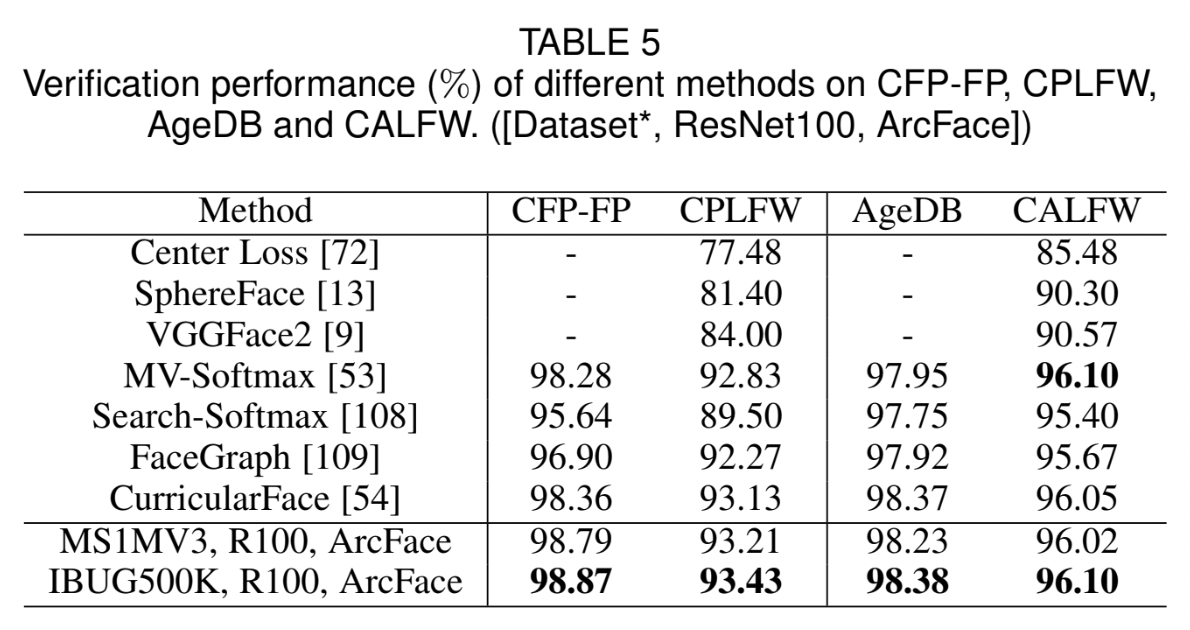
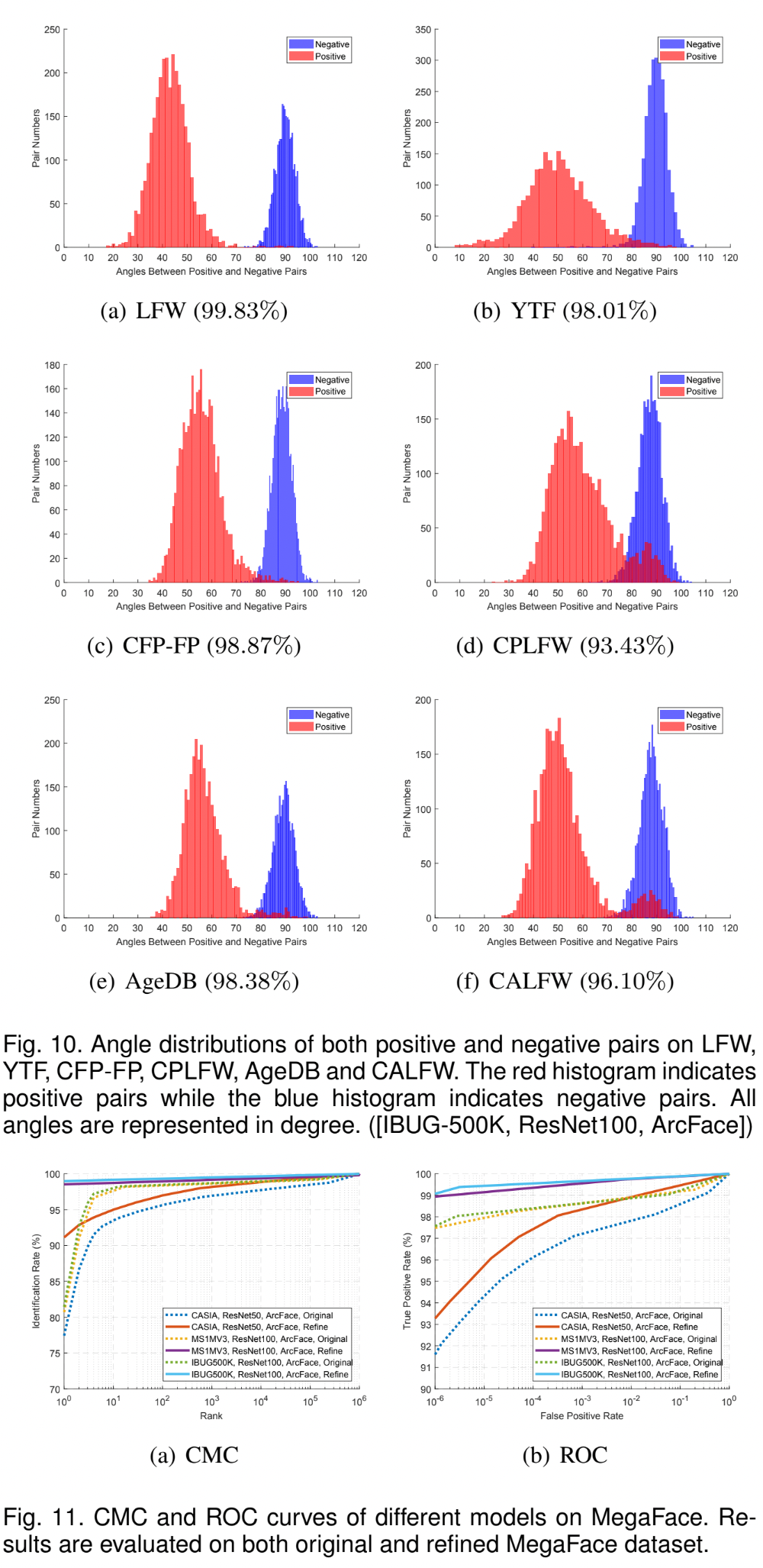
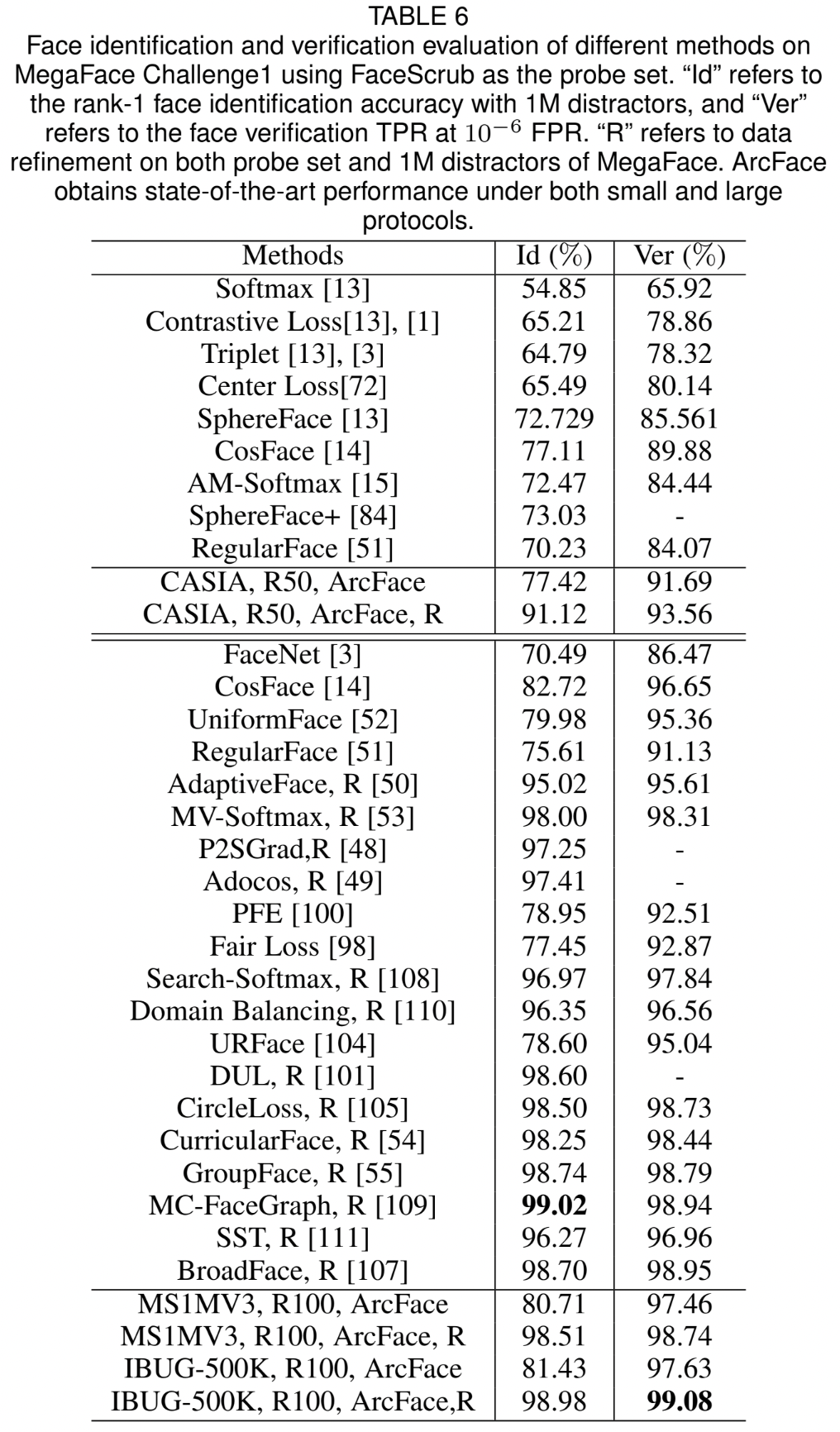
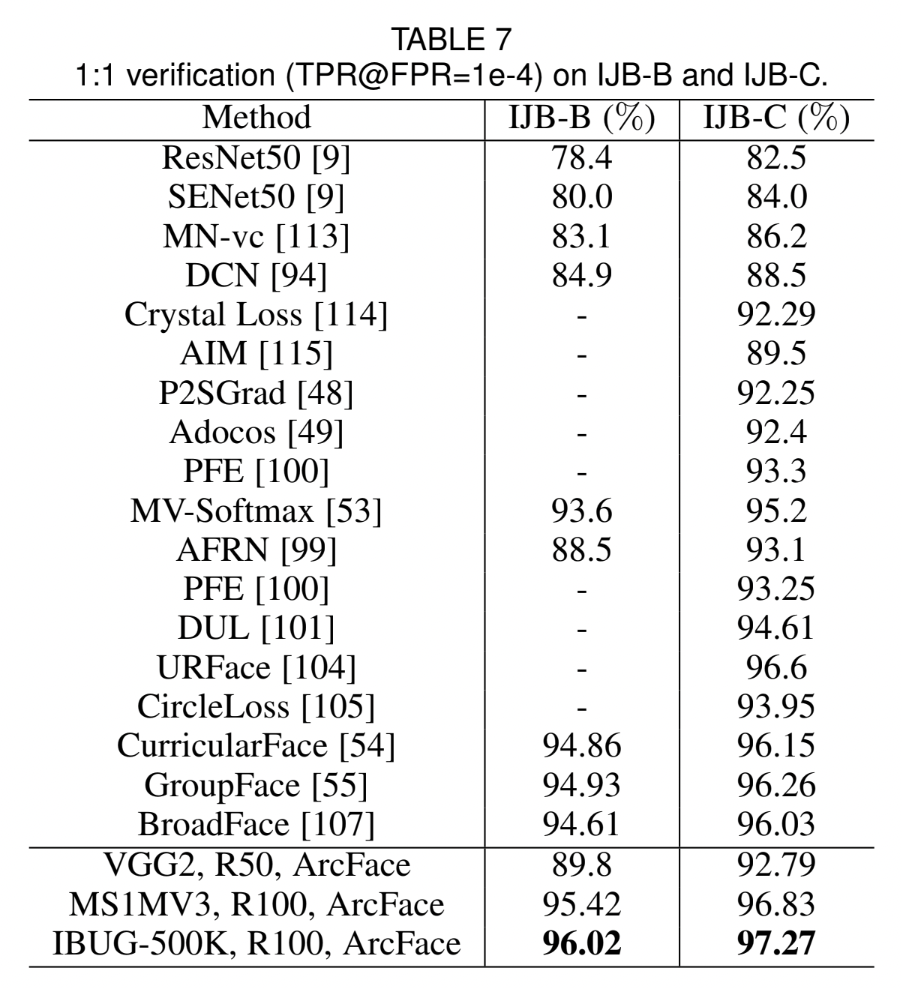
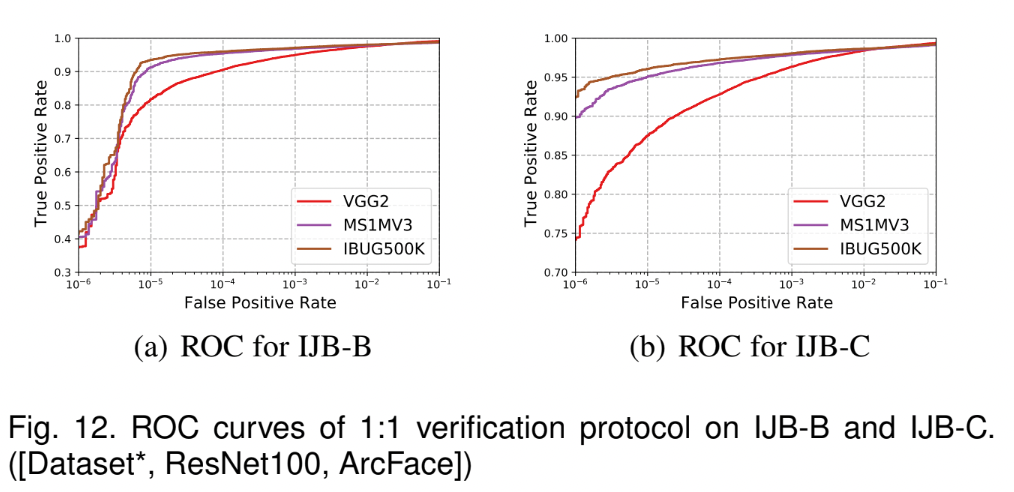
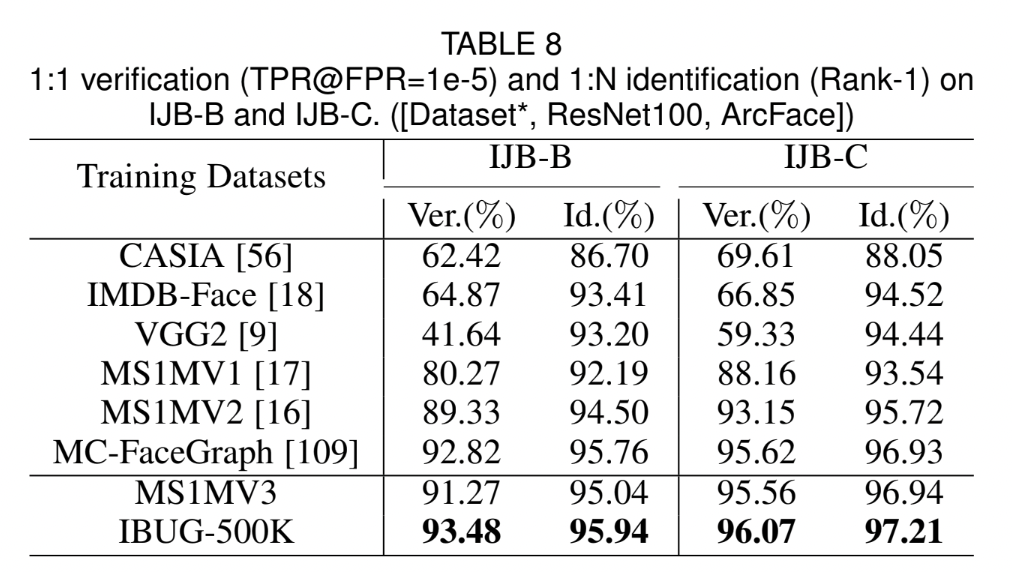
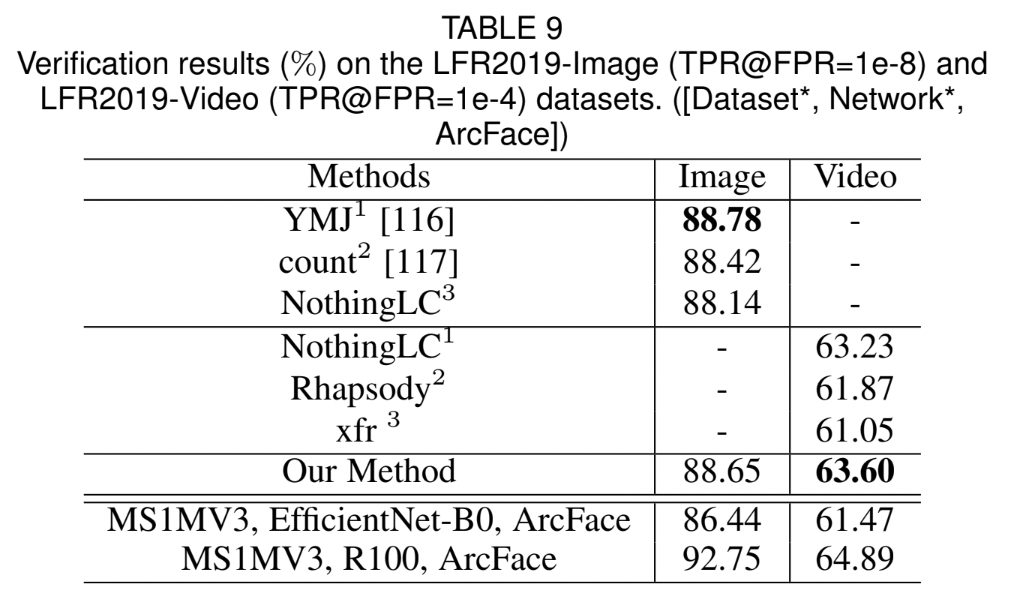
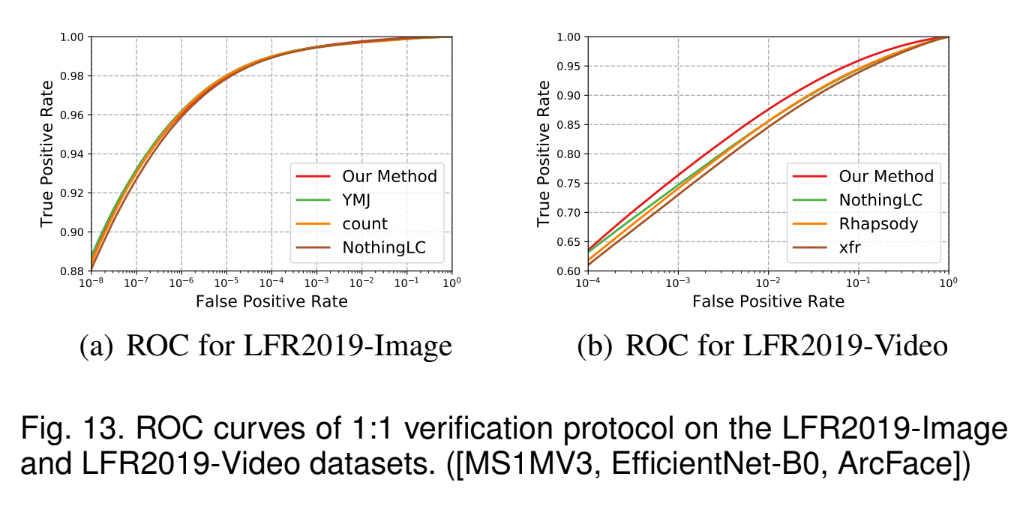
4.4 Benchmark Results

Tables & Graphs

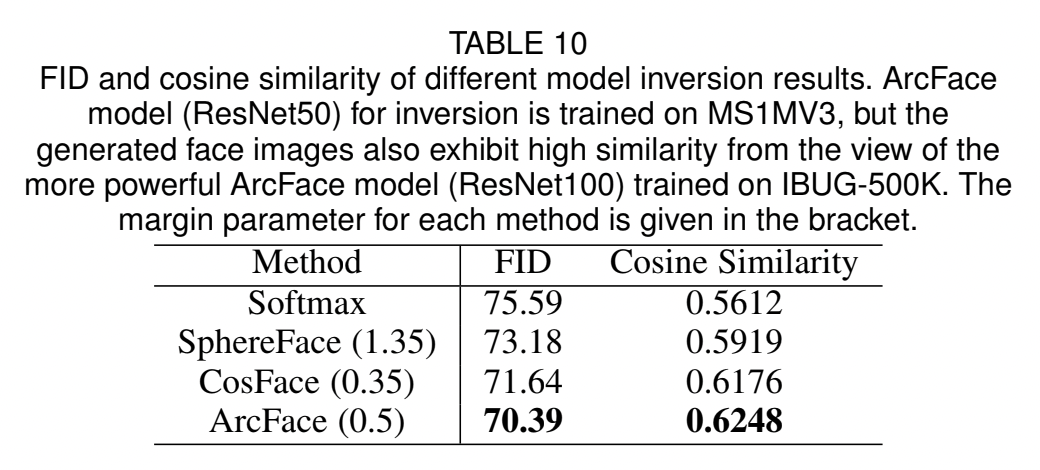
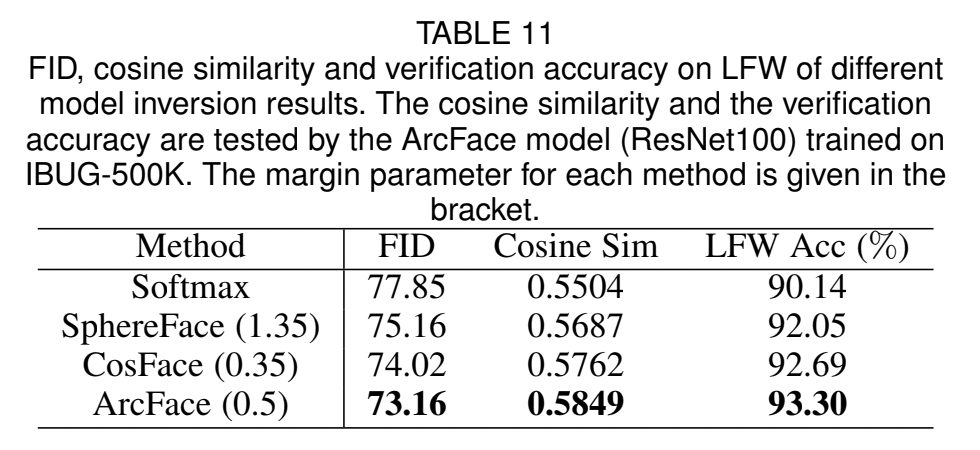
4.5 Inversion of ArcFace

Close-set Face Generation

각 identity에 대해, different random inputs를 입력 후 gradually update 한 결과이다.

Open-set Face Generation

---

5. Conclusions

• face recognition에서 feature embedding에 대해 discriminative power를 효과적으로 향상시킬 수 있는 Additive Angular Margin Loss function(ArcFace)을 제안했다.
• 또한, massive real-world noises에 대응할 수 있는 sub-class ArcFace를 제안했다. 이를 통해 noisy dataset에 대해 automatic isolation이 가능하다.
  • one dominant sub-class = majority of clean faces
  • non-dominant sub-classes = hard or noisy faces
• ArcFace를 통해 feature vectors를 face images로 mapping 하는 generative power를 강화할 수 있다.
  • network gradient와 BN priors만을 이용한다.
  • close-set과 open-set 문제에 대해 모두 적용할 수 있다.