Home [Python] 파이썬의 반올림은 사사오입? 오사오입? (+ 부동 소수점, Decimal)
Post
Cancel

[Python] 파이썬의 반올림은 사사오입? 오사오입? (+ 부동 소수점, Decimal)

Posted Mar 27, 2024 Updated Jul 24, 2024
By Seungri
24 min read

파이썬의 내장 round() 함수는 우리가 흔히 사용하는 “사사오입” 방식의 반올림이 아닌, “오사오입” 방식의 반올림을 제공한다. 오사오입이란 무엇이며 왜 사용하는지, 더 나아가 부동 소수점의 문제점과 이를 해결하는 decimal 모듈까지 살펴보자.

반올림 방식에 대해서는 공식적인 자료를 찾지 못하여 틀린 부분이 있을 수 있음을 밝힙니다.


1. 대표적인 반올림(Rounding) 방식 네 가지

우선, 여러 반올림 방식 중 가장 대표적인 네 가지를 살펴보자.

1-0. 들어가기 전에

  • Round up / Round down
    • round up이란, 양의 방향으로 향하는 것(= more positive)을 의미하며 음수일 때도 마찬가지이다.
    • 반대로 round down이란, 음의 방향으로 향하는 것(= more negative)을 의미한다.

    ref: https://www.geeksforgeeks.org/how-to-round-numbers-in-python/


  • 1-1. Rounding Half Up과 1-2. Rounding Half Down에서 “음수인 경우”에 대한 내용은 정확하지 않을 수 있다. 정확한 자료를 찾지 못했기 때문에, 여러 반올림 방식을 지원하는 계산기를 통해 값을 실제로 구해보고 그 결과를 토대로 작성했다.

    symmetric 방식과 asymmetric 방식이 있는 것 같고, 나는 asymmetric 방식 기준으로 본 포스팅을 작성했다.

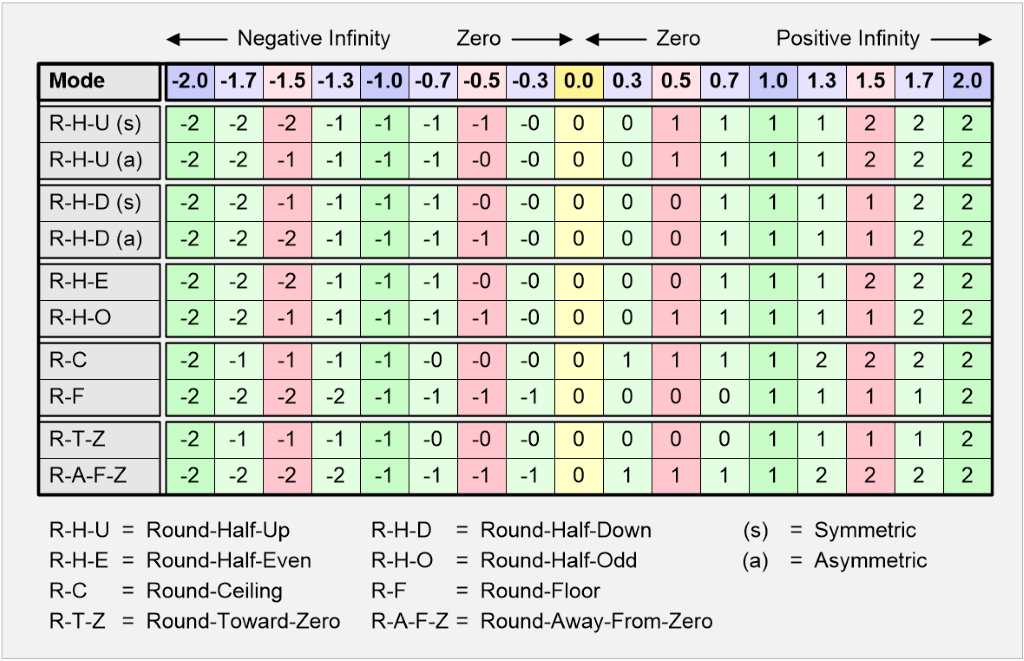    ref: https://www.clivemaxfield.com/coolbeans/fundamentals-different-rounding-algorithms/


  • 이어지는 예시에서는 편의상 반올림 시 고려해야 하는 값을 x라 하고, 주어진 숫자를 반올림하여 소수점 아래 첫째자리까지 나타내도록 하겠다.

    ex) 1.151라는 숫자를 반올림하여 소수점 아래 첫째자리까지 나타낼 때, x는 소수점 아래 둘째자리부터 일의 자리로 설정한 5.1가 된다.


1-1. Rounding Half Up (사사오입) (Asymmetric)

사사오입이란 일반적인 반올림으로, 쉽게 이야기하면 (양수 기준으로) 정확하게 절반에 해당하는 경우 이상을 무조건 올리는 방식이다. “4는 버리고 5는 채택한다”는 뜻이기에, 아래 자리는 절사하고 최소 단위의 바로 밑 자리가 5인지만 검사하면 되므로 간단하다.

참고로, 흔히 사용되는 “사사오입” 방식이란 엄밀하게 말하면 symmetric 방식을 의미하는 것으로 보인다. 본 섹션에서는 asymmetric 방식에 대해 살펴본다.

  • 양수인 경우

    x의 크기동작
    x < 5round down
    x ≥ 5round up

  • 음수인 경우

    x의 크기동작
    x ≤ 5round up
    x > 5round down

  • 예시

    반올림하는 숫자x동작반올림 결과대칭 여부
    1.1515.1 (≥ 5)up1.2 
    1.1505.0 (≥ 5)up1.2asymmetric
    1.1494.9 (< 5)down1.1 
    -1.1494.9 (≤ 5)up-1.1 
    -1.1505.0 (≤ 5)up (more positive)-1.1asymmetric
    -1.1515.1 (> 5)down-1.2 

  • 코드 구현

    1
2
3

    def round_half_up(n, decimals=0):
    multiplier = 10 ** decimals
    return math.floor(n * multiplier + 0.5) / multiplier


1-2. Rounding Half Down (오사육입) (Asymmetric)

오사육입이란 사사오입과는 반대로 절반에 해당하는 경우 이하를 내리는 방식으로, 주로 공모주 청약이나 회계/정책 결정에 사용되는 방식이다.

  • 양수인 경우

    x의 크기동작
    x ≤ 5round down
    x > 5round up

  • 음수인 경우

    x의 크기동작
    x < 5round up
    x ≥ 5round down

  • 예시

    반올림하는 숫자x동작반올림 결과대칭 여부
    1.1515.1 (> 5)up1.2 
    1.1505.0 (≤ 5)down1.1asymmetric
    1.1494.9 (≤ 5)down1.1 
    -1.1494.9 (< 5)up-1.1 
    -1.1505.0 (≥ 5)down (more negative)-1.2asymmetric
    -1.1515.1 (≥ 5)down-1.2 

  • 코드 구현

    1
2
3

    def round_half_down(n, decimals=0):
    multiplier = 10 ** decimals
    return math.ceil(n * multiplier - 0.5) / multiplier


rounding half down과 오사육입은 완전히 동일할까?

흔히 실생활에서 사용되는 “오사육입” 방식이란 “5는 버리고 6은 채택한다”는 뜻으로, 사사오입과 동일하게 아래 자리는 절사한다고 한다. 따라서 다음과 같이 소수점 아래 첫째자리에서 반올림한 결과가 다르다. rounding half down이 오사육입이라고 알려져 있기는 하나, 영문과 국문 용어가 서로 완벽히 호환되는 것 같지는 않다. (오히려 rounding half down은 “사사육입” 방식이라고 볼 수 있을 것 같다.)

반올림하는 숫자❶ rounding half down❷ 실생활에서 사용되는 오사육입
1.6022 (x가 6일 때 비로소 올림)
1.592 (x가 5.9 > 5이므로 올림)1 (x가 5이므로 아래 자리는 절사)


1-3. Rounding Half Away From Zero (Symmetric)

쉽게 생각하면 양수인 경우에는 rounding half up(사사오입), 음수인 경우에는 rounding half down(오사육입)을 사용하는 방법이다. 이렇게 하면 0을 기준으로 symmetric 하게 된다!

ref: https://www.mathsisfun.com/numbers/rounding-methods.html

x의 크기동작
x ≥ 5round away from zero
x < 5round toward zero
반올림하는 숫자x동작반올림 결과대칭 여부
1.1515.1 (≥ 5)away from zero (up)1.2 
1.1505.0 (≥ 5)away from zero (up)1.2symmetric
1.1494.9 (< 5)toward zero (down)1.1 
-1.1494.9 (< 5)toward zero (up)-1.1 
-1.1505.0 (≥ 5)away from zero (down)-1.2symmetric
-1.1515.1 (≥ 5)away from zero (down)-1.2 


1-4. Rounding Half Even (오사오입; Banker’s Rounding) (Symmetric)

자연과학, 공학의 유효숫자 개념이나 컴퓨터에서 많이 사용하는 방식이다.

x의 크기동작
x < 5round toward zero
x = 5round to the nearest even value (between up & down)
x > 5round away from zero

  • 반올림 되는 자리의 숫자가 홀수(1)인 경우 → 가까운 짝수로 변경

    반올림하는 숫자x동작반올림 결과대칭 여부
    1.1515.1 (> 5)away from zero (up)1.2 
    1.1505.0 (== 5)closest even value
    (between 1 and 2)    		1.2symmetric
    1.1494.9 (< 5)toward zero (down)1.1 
    -1.1494.9 (< 5)toward zero (up)-1.1 
    -1.1505.0 (== 5)closest even value
    (between 1 and 2)    		-1.2symmetric
    -1.1515.1 (> 5)away from zero (down)-1.2 

  • 반올림 되는 자리의 숫자가 짝수(2)인 경우 → 그대로 유지

    반올림하는 숫자x동작반올림 결과대칭 여부
    1.2515.1 (> 5)away from zero1.3 
    1.2505.0 (== 5)closest even value
    (between 2 and 3)    		1.2symmetric
    1.2494.9 (< 5)toward zero1.2 
    -1.2494.9 (< 5)toward zero-1.2 
    -1.2505.0 (== 5)closest even value
    (between 2 and 3)    		-1.2symmetric
    -1.2515.1 (> 5)away from zero-1.3 


2. 파이썬의 반올림

그렇다면, 파이썬은 이러한 반올림 방식 중 무엇을 채택하고 있을까?

2-1. 내장 round() 함수: Rounding Half Even

파이썬3에서 제공하는 내장 round() 함수는 rounding half even(오사오입) 방식이다. 참고로 파이썬2에서는 rounding half up(사사오입) 방식이었다고 한다.

파이썬 공식문서 발췌 (바로가기):

Note: The behavior of round() for floats can be surprising: for example, round(2.675, 2) gives 2.67 instead of the expected 2.68. This is not a bug: it’s a result of the fact that most decimal fractions can’t be represented exactly as a float. See Floating Point Arithmetic: Issues and Limitations for more information.


따라서 소수점 아래 첫째자리에서 반올림하는 상황을 가정할 때, 해당 자리의 숫자가 5인 경우를 살펴보면 다음과 같은 결과를 얻게 된다.

1
2
3
4
5
6
7
8
9
10

round(-4.5)	=  -4  # <- ! (-5가 아님)
round(-3.5)	=  -4
round(-2.5)	=  -2  # <- ! (-3이 아님)
round(-1.5)	=  -2
round(-0.5)	=   0  # <- ! (-1이 아님)
round( 0.5)	=   0  # <- ! ( 1이 아님)
round( 1.5)	=   2
round( 2.5)	=   2  # <- ! ( 3이 아님)
round( 3.5)	=   4
round( 4.5)	=   4  # <- ! ( 5가 아님)


그리고 동일한 상황에서 반올림 되는 자리의 값이 홀수일 때와 짝수일 때를 나누어서 살펴보면 다음과 같다.

  • 홀수일 때 (1)

    1
2
3
4
5
6

    round(-1.6)	=  -2
round(-1.5)	=  -2  # <- ! (1과 2 중에서 가까운 짝수인 2로 변경)
round(-1.4)	=  -1
round( 1.4)	=   1
round( 1.5)	=   2  # <- ! (1과 2 중에서 가까운 짝수인 2로 변경)
round( 1.6)	=   2

  • 짝수일 때 (2)

    1
2
3
4
5
6

    round(-2.6)	=  -3
round(-2.5)	=  -2  # <- ! (2와 3 중에서 가까운 짝수인 2로 변경)
round(-2.4)	=  -2
round( 2.4)	=   2
round( 2.5)	=   2  # <- ! (2와 3 중에서 가까운 짝수인 2로 변경)
round( 2.6)	=   3

이러한 원리로 파이썬에서는 round(2.5)와 round(1.5)가 모두 동일하게 2로 계산되는 것이다.


파이썬에서는 다음과 같이 우리가 흔히 생각하는 방식으로 반올림이 수행되지 않는다는 것에 주의하자!

1
2
3
4
5
6
7
8

round(-4.5)	=  -5
round(-3.5)	=  -4
round(-2.5)	=  -3
round(-1.5)	=  -2
round( 1.5)	=   2
round( 2.5)	=   3
round( 3.5)	=   4
round( 4.5)	=   5


2-2. Rounding Half Even(오사오입)의 도입 이유

일상에서 사용하는 rounding half up(사사오입)이 훨씬 간단하고 직관적인 것 같은데, 왜 공학/자연과학/컴퓨터 분야에서는 rounding half even(오사오입)을 사용할까?

이는 컴퓨터가 사용하는 이진수에서 소수를 부동 소수점(floating-point) 방식(다음 섹션에서 설명)으로 표현하기 때문이다. 대부분의 경우, 십진 부동 소수점 수를 이진 부동 소수점 수로는 정확하게 표현할 수 없기 때문에 필연적으로 오차가 발생하게 된다. 이때, 사사오입 방식을 사용하면 항상 양의 무한대 방향으로 올림이 되므로 오차가 해당 방향으로 편향되어 나타날 수밖에 없다. 하지만 값에 따라 올림과 내림을 수행하는 오사오입 방식을 적용하면 오차의 편향(bias)을 최대한 줄일 수 있다.

또한, 통계학적으로도 근사치를 바탕으로 통계를 내는 경우에는 오사오입의 오차가 작아 합리적이라고 한다. 물론 오사오입으로 인해 확률 분포가 짝수 쪽으로 증가하겠지만, 이는 근사치를 사용할 때 편향이 생기는 것에 비해 덜 치명적이다.

오사오입이 통계학적으로 합리적인 반올림 방법인 이유: 참고 자료


2-3. 파이썬에서 사사오입으로 반올림하는 방법 (Symmetric)

일반적으로 사용되는 사사오입 방식인 symmetric rounding half up으로 소수 첫째자리에서 반올림 하는 경우를 가정한다.

  1. 함수 직접 작성하기

    1
2
3
4
5

     def round_half_up(value):
     if value >= 0:
         return int(value + 0.5)
     else:
         return int(value - 0.5)

    1
2
3
4
5
6

     round_half_up(-0.51) = -1
 round_half_up(-0.50) = -1
 round_half_up(-0.49) =  0
 round_half_up( 0.49) =  0
 round_half_up( 0.50) =  1
 round_half_up( 0.51) =  1

  2. decimal 모듈 사용하기

    • 첫 번째 방법: Decimal.quantize(value, ROUND_HALF_UP)

      1
2
3
4

      from decimal import Decimal, ROUND_HALF_UP

def round_half_up(value):
    return Decimal(num).quantize(0, ROUND_HALF_UP)

      1
2
3
4
5
6

      round_half_up(-0.51) = -1
round_half_up(-0.50) = -1
round_half_up(-0.49) = -0
round_half_up( 0.49) =  0
round_half_up( 0.50) =  1
round_half_up( 0.51) =  1

    • 두 번째 방법: Decimal(num).to_integral_value(rounding=ROUND_HALF_UP)

      1
2

      def round_half_up(value):
    return Decimal(num).to_integral_value(rounding=ROUND_HALF_UP)

      1
2
3
4
5
6

      round_half_up(-0.51) = -1
round_half_up(-0.50) = -1
round_half_up(-0.49) = -0
round_half_up( 0.49) =  0
round_half_up( 0.50) =  1
round_half_up( 0.51) =  1


3. decimal 모듈

앞서 파이썬에서 사사오입으로 반올림하는 방법을 살펴보면서 decimal 모듈을 잠깐 다루었다. decimal 모듈은 무슨 기능을 제공하며, 어떠한 이유로 파이썬에 도입되었을까?

3-1. 컴퓨터에서 부동 소수점(Floating-Point) 수를 다룰 때의 문제점

컴퓨터는 부동 소수점 수를 이진수로 표현한다.

ex) 십진 소수(decimal fraction) 0.625가 6/10 + 2/100 + 5/1000의 값을 가지듯이, 이진 소수(binary fraction) 0.101은 1/2 + 0/4 + 1/8의 값을 가지는 것이다. 두 소수는 동일한 값을 가지나, 전자는 십진법으로, 후자는 이진법으로 나타내었다는 점만 다르다.

하지만 대부분의 십진 소수는 이진 소수로 정확하게 표현될 수 없으며, 이에 따라 십진 부동 소수점 수가 실제로 컴퓨터에 저장될 때는 이진 부동 소수점 수로 근사된다. 일례로, 십진 소수 0.1을 이진 소수로 나타내면 다음과 같이 무한히 반복되는 값을 확인할 수 있다.

1

0.0001100110011001100110011001100110011001100110011...

즉, 위와 같은 수를 컴퓨터에서 표현하기 위해서는 유한한 비트 수에서 잘라야 하고, 그렇게 되면 근사치를 얻게 되는 것이다. 파이썬 또한 예외가 아니기에 종종 다음과 같이 당황스러운 결과를 얻게 된다.

1
2
3
4
5

0.1 * 7 - 0.7
# 1.1102230246251565e-16

0.3 + 0.3 + 0.3 == 0.9
# False


이처럼 컴퓨터에서 이진 부동 소수점 타입인 float 관련 연산을 할 때에는 항상 (1) 십진 연산이 아니라는 점과 (2) 반올림 오류가 발생할 수 있다는 점에 유의해야 한다.

앞서 언급했듯, 이러한 부동 소수점 문제는 컴퓨터 분야에서 반올림 방식으로 주로 오사오입을 채택하는 이유와도 관련이 있다!


그렇다면 여기에서 의문이 들 것이다. 대부분의 경우에는 특정 자릿수로 반올림 하면 기대하는 결과를 볼 수 있겠지만, 정확한 십진 연산이 필요한 경우에는 어떻게 대처해야 하는 걸까? 바로 여기에서 decimal 모듈이 등장한다!


3-2. decimal: 정확한 십진 소수 연산을 위한 모듈

파이썬의 decimal 모듈은 십진 부동 소수점 연산을 위한 Decimal 데이터 타입을 제공한다.

이러한 Decimal 타입은 내장 float 이진 부동 소수점 타입과 비교했을 때, 다음과 같이 정확한 연산이 필요한 경우에 유용하다.

  1. 정확한 십진수 표현이 필요한 금융/재무/회계 관련 애플리케이션
  2. 정밀도 제어
  3. 법적 또는 규제 요구 사항을 충족하는 반올림 제어
  4. 유효숫자 추적
  5. 사용자가 손으로 계산한 결과와 일치할 것으로 기대하는 값


다음과 같은 몇 가지 예시를 살펴보면, Decimal 타입을 사용한 결과가 우리가 예상한 값과 일치한다는 것을 알 수 있다.

  1. 70센트 요금에 5%의 세금 부가한 결과를 각각 Decimal과 float 타입으로 계산 후 round()로 반올림하면, 다음과 같이 상이한 결과를 볼 수 있다.

    1
2
3
4
5
6
7
8
9

    from decimal import *

# <1> Decimal 타입: 십진 부동 소수점 연산
round(Decimal("0.70") * Decimal("1.05"), 2)
# Decimal('0.74')

# <2> float 타입: 이진 부동 소수점 연산
round(.70 * 1.05, 2)
# 0.73

  2. 이진 부동 소수점을 사용할 때는 정확한 값을 얻을 수 없었던 나머지 연산이나 동등성 비교를 정확하게 수행할 수 있다.

    1
2
3
4
5
6
7

    # <1> Decimal 타입: 십진 부동 소수점 연산
Decimal("1.00") % Decimal(".10")
# Decimal('0.00')

# <2> float 타입: 이진 부동 소수점 연산
1.00 % 0.10
# 0.09999999999999995

    1
2
3
4
5
6
7

    # <1> Decimal 타입: 십진 부동 소수점 연산
sum([Decimal("0.1")] * 10) == Decimal("1.0")
# True

# <2> float 타입: 이진 부동 소수점 연산
0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 == 1.0
# False


간단하게 정리하면 Decimal을 통해 사람이 손으로 계산한 결과와 동일한 결과를 얻을 수 있으며, 이진 부동 소수점이 십진수를 정확하게 표현할 수 없을 때 발생 가능한 문제를 예방할 수 있다.

1
2
3
4
5

Decimal("0.1") * 7 - Decimal("0.7")
# Decimal('0.0')

Decimal("0.3") + Decimal("0.3") + Decimal("0.3") == Decimal("0.9")
# True


3-3. decimal 모듈 사용 시 주의사항

  1. Decimal 객체 생성 시, value 값을 str 타입으로 넘겨야 한다.

    str 타입이 아닌 float 타입으로 넘기면 float 연산에서 발생했던 문제점이 그대로 나타난다. 이는 이진 부동 소수점 값이 손실 없이 정확한 십진수로 변환되기 때문이다.

  2. Decimal은 정확한 십진 연산이 필요한 경우에는 적합하나, 성능 및 메모리 측면에서 트레이드 오프가 발생한다.

    반드시 필요한 경우가 아니라면 성능을 위해 float를 사용하는 것을 권장한다.

  3. 모든 모듈 및 라이브러리가 Decimal 객체를 지원하는 것은 아니므로 호환성에 문제가 발생할 수 있다.


decimal과 관련된 더 자세한 내용은 다음의 자료를 참고하자.


References

Python, More About Python
python round floating point binary decimal float
This post is licensed under CC BY 4.0 by the author.
Recently Updated
Contents

[Python] 간편하게 행렬 뒤집기 & 회전하기 (+ zip(), [::-1])

[Algorithm] Quick Select: K 번째 원소 찾기